
【题目】两条直线y1=ax+b与y2=bx+a(a≠0,b≠0)在同一平面直角坐标系中的图象可能是( )
A.  B.
B. 
C.  D.
D. 
【答案】A
【解析】
根据一次函数的性质可依次作判断.
解:A、由y1=ax+b知:a>0,b<0,所以y2=bx+a交y轴正半轴,过一、二、四象限,符合y2=bx+a的图象,故此选项正确;
B、由y1=ax+b知:a>0,b>0,所以y2=bx+a应交y轴正半轴,过一、二、三象限,不符合y2=bx+a的图象,故此选项错误;
C、由y1=ax+b知:a>0,b<0,所以y2=bx+a应交y轴正半轴,过一、二、四象限,不符合y2=bx+a的图象,故此选项错误;
D、由y1=ax+b知:a>0,b>0,所以y2=bx+a应交y轴正半轴,过一、二、三象限,不符合y2=bx+a的图象,故此选项错误;
故选:A.


科目:初中数学 来源: 题型:
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书, 然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离 s(千米)与离家的时间 t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为 千米,书店离家的距离为_____千米;王亮同学在书店待了______分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
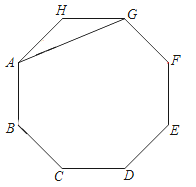
【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
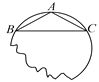
【题目】如图,要把残破的轮片复制完整,已知弧上的三点A、B、C.
(1)用尺规作图法找出![]() 所在圆的圆心(保留作图痕迹,不写作法);
所在圆的圆心(保留作图痕迹,不写作法);
(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
查看答案和解析>>
科目:初中数学 来源: 题型:
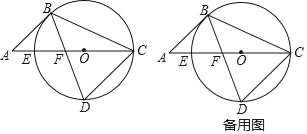
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 内接于半圆,
内接于半圆,![]() 是直径,过
是直径,过![]() 作直线
作直线![]() ,
,![]() ,
,![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
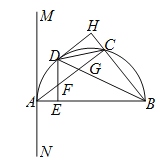
(![]() )求证:
)求证:![]() 是半圆的切线.
是半圆的切线.
(![]() )作
)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() ,
,![]() ,试求
,试求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
(1)点A坐标为______;点B坐标为______;点C坐标为______;
(2)画出△ABC关于原点对称的△A1B1C1;
(3)已知M(1,4),在x轴上找一点P,使|PM-PB|的值最大(写出过程,保留作图痕迹),并写出点P的坐标______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com