
【题目】如图,![]() 内接于半圆,
内接于半圆,![]() 是直径,过
是直径,过![]() 作直线
作直线![]() ,
,![]() ,
,![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(![]() )求证:
)求证:![]() 是半圆的切线.
是半圆的切线.
(![]() )作
)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() ,
,![]() ,试求
,试求![]() 的长.
的长.
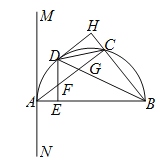
【答案】(1)答案见解析;(2)AE=CH;(3)1.
【解析】试题分析:(1)由AB是直径得出∠ACB=90°,推出∠CAB+∠MAC=90°即可;
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
试题解析:解:(1)如图所示.∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°.∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,即∠MAB=90°,∴MN是半圆的切线;

(2)AE=CH.理由如下:
连接AD.∵D是弧AC的中点,∴AD=CD,∠HBD=∠ABD.∵DE⊥AB,DH⊥BC,∴DE=DH,∠AED=∠DHC,在Rt△ADE和Rt△CDH中,∵AD=CD,DE=DH,∴Rt△ADE≌Rt△CDH(HL),∴AE=CH;

(3)由(2)知DH=DE,∠DHB=∠DEB=90°,在Rt△DBH和Rt△DBE中,∵DH=DE,BD=BD,∴Rt△DBH≌Rt△DBE(HL),∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,又∵AB=6,BC=4,∴6﹣AE=4+AE,∴AE=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 和
和![]() 两点.
两点.
观察图象可知:①当![]() 或
或![]() 时,
时,![]() ;②当
;②当![]() 或
或![]() 时,
时,![]() ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式![]() 的解集.
的解集.
有这样一个问题:求不等式![]() 的解集.
的解集.
某同学根据学习以上知识的经验,对求不等式![]() 的解集进行了探究.
的解集进行了探究.
下面是他的探究过程,请将(![]() )、(
)、(![]() )、(
)、(![]() )补充完整:
)补充完整:
(![]() )将不等式按条件进行转化:
)将不等式按条件进行转化:
当![]() 时,原不等式不成立.
时,原不等式不成立.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
(![]() )构造函数,画出图象.
)构造函数,画出图象.
设![]() ,
,![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
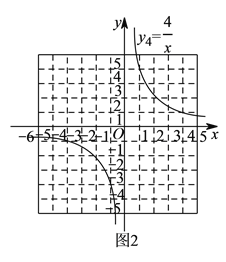
双曲线![]() 如图
如图![]() 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线![]() .(不用列表)
.(不用列表)
(![]() )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足![]() 的所有
的所有![]() 的值为__________.
的值为__________.
(![]() )借助图象,写出解集.
)借助图象,写出解集.
结合(![]() )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式![]() 的解集为__________.
的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满金陵”慈善一日捐活动中,学校团总支为了了解本校写生的捐款情况,随机抽取了![]() 名学生的捐款数进行了统计,并绘制成统计图.
名学生的捐款数进行了统计,并绘制成统计图.
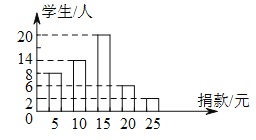
(![]() )这
)这![]() 名同学捐款的众数为__________元,中位数为__________.
名同学捐款的众数为__________元,中位数为__________.
(![]() )求这
)求这![]() 名同学捐款的平均数.
名同学捐款的平均数.
(![]() )该校共有
)该校共有![]() 名学生参与捐款,请估计该校学生的捐款总数.
名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在“圣诞节”来临前夕,购进一种品牌巧克力,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元,根据以往销售经验发现;当售价定为每盒
元,根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价提高
盒,每盒售价提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
(![]() )试求出每天的销售量
)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(![]() )当每盒售价定为多少元时,每天销售的利润
)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(![]() )为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于
)为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于![]() 元.如果超市想要每天获得不低于
元.如果超市想要每天获得不低于![]() 元的利润,那么超市每天至少销售巧克力多少盒?
元的利润,那么超市每天至少销售巧克力多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空,如图:方格纸中每个小正方形的边长都为 1,![]() 的顶点都在方格纸的格点上,
的顶点都在方格纸的格点上,
将 ![]() 经过一次平移后得到
经过一次平移后得到 ![]() .图中标 出了点
.图中标 出了点 ![]() 的对应点
的对应点 ![]() .
.
(1)请画出平移后的![]() ;
;
(2)若连接 ![]() ,
, ![]() ,则这两条线段的关系是_____;
,则这两条线段的关系是_____;
(3)利用网格画出 ![]() 中
中 ![]() 边上的中线
边上的中线 ![]() 以及
以及![]() 边上的高
边上的高 ![]() ;
;
(4)线段 ![]() 在平移过程中扫过区域的面积为 _____.
在平移过程中扫过区域的面积为 _____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com