
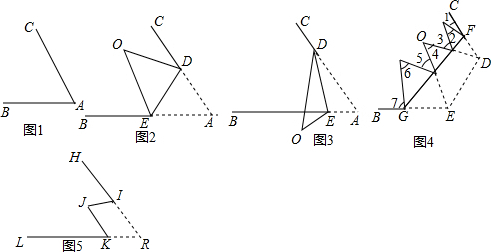
分析 (1)由平角和对折的性质简单计算∠CDO=180°-2∠ADE即可;
(2)由平角和对折的性质简单计算∠OEB=∠AED-180°即可;
(3)由对折和平角的意义进行简单的计算,
(3)利用几何图形,对折,平角的意义简单的计算.
解答 解:(1)∵如图2,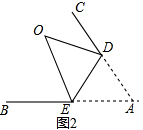
∵把三角形纸片ABC的∠A沿DE折起,点A的对称点为点O,
∴∠CDO+∠OEB
=(180°-2∠ADE)+(180°-2∠AED)
=2(180°-∠ADE-∠AED)=2α;
(2)∠CDO-∠OEB=2α,
理由如下:如图3,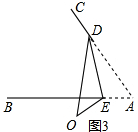
∠CD0-∠OEB
=(180°-2∠ADE)-(2∠AED-180°)
=2(180°-∠ADE-∠AED)
=2α;
(3)∠CFP+PMO+∠ONQ+∠QGB=4α,
理由如下:如图4,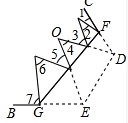
∠CFP+∠PMO+∠ONQ+∠QGB
=(∠CFP+∠PMO)+(∠ONQ+QGB)
=2∠FDM+2∠NEG
=2(∠FDM+NEG)
=4∠BAC
=4α;
(4)∠HRL=∠IJK,
理由如下:如图5,连接JR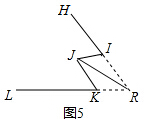
∵∠HIJ+∠JKL
=(∠IRJ+∠IJR)+(∠KRJ+∠KJR)
=(∠IJR+∠KJR)+(∠IRJ+∠KRJ)
=∠IJK+∠IRK
=2∠IJK,
∴∠HRL=∠IJK.
点评 本题是几何变换题,主要考查了对折的性质,本题的关键是从复杂图形分离出有用的部分,本题易出错的地方是,写错角.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
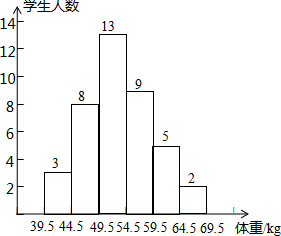 根据某班40名同学的体重频数分布直方图,回答下列问题:
根据某班40名同学的体重频数分布直方图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
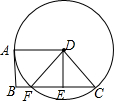 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com