
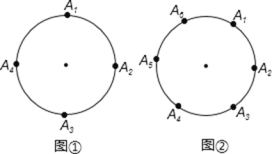
【题目】如图①,如果 A1、A2、A3、A4 把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形4个;如图②,如果A1、A2、A3、A4、A5、A6 把圆周六等分,则以A1、A2、A3、A4、A5、A6 为点的直角三角形有 12 个;如果 A1、A2、A3、……A2n 把圆周 2n 等分,则以 A1、A2、A3、…A2n为顶点的直角三角形有__________个,
【答案】2n(n-1)
【解析】
根据圆周角定理找到直径所对的圆周角是直角,然后由一条直径所对的直角数来寻找规律.
![]() 解:由圆周角定理知,直径所对的圆周角是直角.
解:由圆周角定理知,直径所对的圆周角是直角.
∴当A1、A2、A3、A4把圆周四等分时,该圆中的直径有A1A3,A2A4两条,
∴①当以A1A3为直径时,有两个直角三角形;
②当以A2A4为直径时,有两个直角三角形;
∴如果A1、A2、A3、A4把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形有(4÷2)×(4-2)=4个;
当A1、A2、A3、A4、A5、A6把圆周六等分,则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有(6÷2)×(6-2)=12个;
当A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有(2n÷2)×(2n-2)=2n(n-1)个.
故答案是:2n(n-1).


科目:初中数学 来源: 题型:
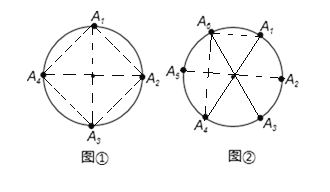
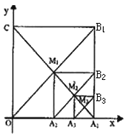
【题目】如图 ,在平面直角坐标系中,边长为 1 的正方形OA1B1C 的对角线 A1C 和OB1 交于点 M1,以 M1A1为对角线作第二个正方形 A2A1B2M1对角线 A1M1和 A2 B2 交于点 M 2 ;以 M 2 A1 为对角线作第三个正方形 A3 A1B3M 2,对角线 A1M 2 和 A3 B3 交于点 M 3 ;…,依此类推,那么 M 1 的坐标为_____;这样作的第 n 个正方形的对角线交点 Mn 的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
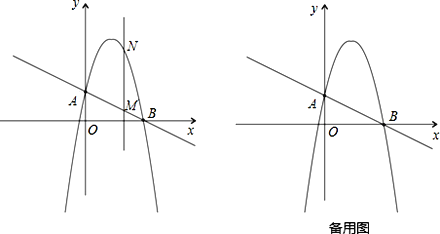
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.
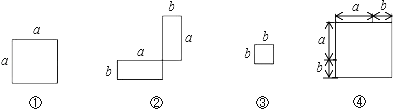
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念李时珍诞辰500周年,蕲春县投巨资建设如图所示展览馆,其外框是一个大正方形,中间四个大小相同的正方形(阴影部分)是支展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的图形是休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米
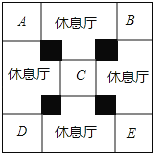
(1)若设展厅的正方形边长为a米,则用含a的代数式表示核心筒的正方形边长为 米.
(2)若设核心筒的正方形边长为b米,求该展馆外框大正方形的周长(用含b的代数式表示).
(3)若展览馆外框大正形边长为26米,求休息厅的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 在平面直角坐标系中的位置如图所示,其中每 个小正方形的边长为 1 个单位长度.
(1)画出△ABC 关于原点 O 的中心对称图形△A1B1C1,并写出点 A1 的坐标;
(2)将△ABC 绕点 C 顺时针旋转 90°得到△A2B2C,画出△A2B2C,求在旋转过程中,点 A 所经过的路径长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
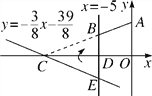
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.
小明画出树状图如图所示:
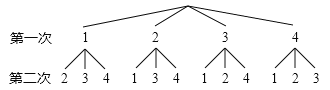
小华列出表格如下:

回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com