
����Ŀ��ij��������һ�������ƽ��ÿ�������100����ÿ��ӯ��30Ԫ.��Ӫ���η��֣�����Ʒÿ������1Ԫ������ƽ��ÿ��ɶ��۳�10��.��ÿ����Ʒ����![]() Ԫʱ����ӯ��Ϊ
Ԫʱ����ӯ��Ϊ![]() Ԫ.�ݴ˹��ɣ�����������⣺
Ԫ.�ݴ˹��ɣ�����������⣺
��1�����ۺ�ÿ����Ʒӯ�� Ԫ������������������ �����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������������£���ÿ����Ʒ���۶���Ԫʱ�����е���ӯ��������Ϊ����Ԫ��
���𰸡���1��(30-x);10x����2��ÿ����Ʒ����10Ԫʱ���̳���ӯ��������ֵ��4000Ԫ.
��������
��1�����ۺ��ӯ������ԭ��ÿ����ӯ����ȥ���͵�Ǯ����������1Ԫ������ƽ��ÿ��ɶ��۳�10������xԪ������ƽ��ÿ��ɶ��۳�10x����
��2��������ϵΪ��ÿ����Ʒ��ӯ������������Ʒ�ļ���=����w����Ϊһ��ʽ�����䷽�ɵó����ۣ�
�⣺��1�����ۺ�ÿ����Ʒӯ��(30-x)Ԫ��������������������10x����
��2����ÿ����Ʒ����xԪʱ������ΪwԪ
��������ã�w=(30x)(100+10x)= 10x2+200x+3000=-10(x-10)2+4000
��10<0����w�����ֵ��
��x=10ʱ���̳���ӯ��������ֵ��4000Ԫ��
��ÿ����Ʒ����10Ԫʱ���̳���ӯ��������ֵ��4000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
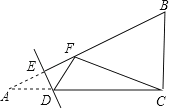
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬AC��8��BC��6����E��AB����һ���㣬����E��DE��AB��AC���ڵ�D������A��ֱ��DE���ۣ���A�����߶�AB�ϵ�F��������FC������BCFΪ����������ʱ��AE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
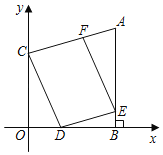
����Ŀ����ͼ����֪��A��7��8����C��0��6����AB��x�ᣬ����Ϊ��B����D���߶�OB�ϣ�DE��AC����AB�ڵ�E��EF��CD����AC�ڵ�F��
��1����A��C�����ֱ�ߵı���ʽ��
��2����OD��t��BE��s����s��t�ĺ�����ϵʽ��
��3���Ƿ���ڵ�D��ʹ�ı���CDEFΪ���Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
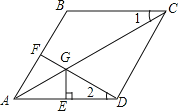
����Ŀ����֪����ͼ��������ABCD�У�FΪ��AB���е㣬DF��Խ���AC���ڵ�G����G��GE��AD�ڵ�E����AB��2���ҡ�1����2�������н�����һ����������_____����������ȷ���۵���Ŷ����ں����ϣ�����DF��AB����CG��2GA����CG��DF+GE����S�ı���BFGC��![]() ��1��
��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У��ᡢ�����궼Ϊ�����ĵ��Ϊ���㣮��֪һ�������ε��ĸ�����ǡ���������������ϣ�����۲�ÿ���������������ϵ�����ĸ����ı仯���ɣ��ش��������⣺
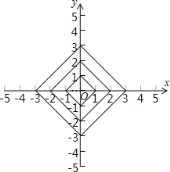
(1)����x���ϵ�(5��0)�������ε��������ϵ����������________��
(2)����x���ϵ�(n��0)(nΪ������)�������ε��������ϵ��������Ϊ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
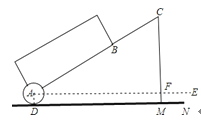
����Ŀ��һ������ʽ�������ʾ��ͼ��ͼ��ʾ�����峤AB=50cm����������쳤����BC=35cm������A��B��C��ͬһ��ֱ���ϣ���������ĵ�װ��һԲ�ι��֡�A����A��ˮƽ�������ڵ�D��AE��DN��ijһʱ�̣���B����ˮƽ��38cm����C����ˮƽ��59cm��
��1����Բ�ι��ֵİ뾶AD�ij���
��2�����˵�����Ȼ�´���������ʱ���˸о���Ϊ�������֪ij�˵�����Ȼ�´��ڵ�C�������˴ﵽ����������ʱ����C����ˮƽ����73.5cm�����ʱ��������ˮƽ��AE���ɽǡ�CAE�Ĵ�С����ȷ��1�㣬�ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.19����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
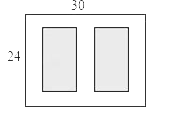
����Ŀ����ͼ��ijС����һ�鳤Ϊ30m����Ϊ24m�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ480m2�������̵�֮�估�ܱ��п�����ȵ�����ͨ����������ͨ���Ŀ���Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
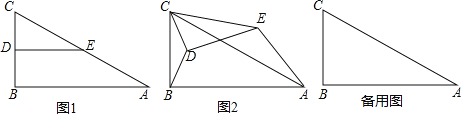
��ͼ1����Rt��ABC�У���B��90����AB��4��BC��2����D��E�ֱ��DZ�BC��AC���е㣬����DE������CDE�Ƶ�C��ʱ�뷽����ת������ת��Ϊ����
��1�����ⷢ��
��������0��ʱ��![]() ���� ������������180��ʱ��
���� ������������180��ʱ��![]() ���� ����
���� ����
��2����չ̽��
���жϣ���0�������360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3��������
��CDE�Ƶ�C��ʱ����ת��A��B��E������ͬһ��ֱ����ʱ�����߶�BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
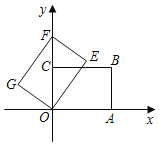
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A��C���������ϣ���A������Ϊ(4��0)����C������Ϊ(0��3)��������OABC�Ƶ�O��ʱ����ת�õ�����OEFG����B�Ķ�Ӧ��Fǡ������y���������ϣ�������OEFG��y������ƽ�ƣ�����E����x����ʱ���˶�ֹͣ����ƽ�Ƶľ���Ϊm���������ص����ΪS��
��1�����E�����ꣻ
��2����S��m�ĺ�����ϵʽ����ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com