
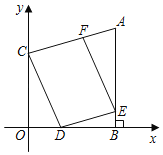
【题目】如图,已知点A(7,8)、C(0,6),AB⊥x轴,垂足为点B,点D在线段OB上,DE∥AC,交AB于点E,EF∥CD,交AC于点F.
(1)求经过A、C两点的直线的表达式;
(2)设OD=t,BE=s,求s与t的函数关系式;
(3)是否存在点D,使四边形CDEF为矩形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+6;(2)s=2﹣
x+6;(2)s=2﹣![]() t(0<t<7);(3)点D的坐标为(
t(0<t<7);(3)点D的坐标为(![]() ,0).
,0).
【解析】
(1)将点A、C的坐标代入一次函数表达式y=kx+b,即可求解;
(2)根据题意可得点D(t,0),点E(7,s),根据一次函数的图象及性质,可得直线DE的表达式为:y=![]() x﹣
x﹣![]() t,将点E的坐标代入即可求解;
t,将点E的坐标代入即可求解;
(3)设点D(t,0),证明∠OCD=∠BDE,则tan∠OCD=tan∠BDE,列出比例式即可求解.
解:(1)设直线AC的表达式为y=kx+b
将点A、C的坐标代入,得
得:![]() ,
,
解得:![]() ,
,
故直线AC的表达式为:y=![]() x+6;
x+6;
(2)∵OD=t,BE=s,AB⊥x轴
∴则点D(t,0),点E(7,s)
∵DE∥AC
可设直线DE的解析式为y=![]() x+c
x+c
将点D的坐标代入
0=![]() t+c
t+c
解得:c=﹣![]() t
t
∴直线的表达式为:y=![]() x﹣
x﹣![]() t,
t,
将点E的坐标代入,得s=2﹣![]() t(根据点D在线段OB上,可得0<t<7);
t(根据点D在线段OB上,可得0<t<7);
(3)存在,理由:
设点D(t,0),由(2)BE=2﹣![]() t,
t,
四边形CDEF为矩形,则∠CDE=90°,
∵∠EDB+∠CDO=90°,∠CDO+∠OCD=90°,
∴∠OCD=∠BDE,
∴tan∠OCD=tan∠BDE,
∴![]() =
=![]()
即![]() =
=![]() ,
,
解得:t=![]() 或7(因为0<t<7,故舍去7),
或7(因为0<t<7,故舍去7),
故点D的坐标为(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】材料1:如图1,昌平南环大桥是经典的悬索桥,当今大跨度桥梁大多采用此种结构.此种桥梁各结构的名称如图2所示,其建造原理是在两边高大的桥塔之间,悬挂着主索,再以相应的间隔,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,主索几何形态近似符合抛物线.

图1
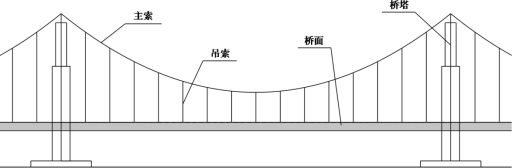
图2
材料2:如图3,某一同类型悬索桥,两桥塔AD=BC=10 m,间距AB为32 m,桥面AB水平,主索最低点为点P,点P距离桥面为2 m;

图3
为了进行研究,甲、乙、丙三位同学分别以不同方式建立了平面直角坐标系,如下图:
甲同学:以DC中点为原点,DC所在直线为x轴,建立平面直角坐标系;

乙同学:以AB中点为原点,AB所在直线为x轴,建立平面直角坐标系;

丙同学:以点P为原点,平行于AB的直线为x轴,建立平面直角坐标系.
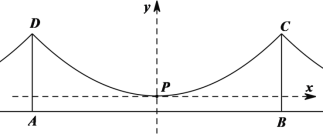
(1)请你选用其中一位同学建立的平面直角坐标系,写出此种情况下点C的坐标,并求出主索抛物线的表达式;
(2)距离点P水平距离为4 m和8 m处的吊索共四条需要更换,则四根吊索总长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A出发,沿边AB向终点B移动,同时点Q从点B出发,沿边BC向终点C移动.已知点P,Q的移动速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为xs.
(1)当x为何值时,四边形APQC的面积等于20![]() ?
?
(2)当x为何值时,△PBQ与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种书包,平均每天可销售100件,每件盈利30元.试营销阶段发现:该商品每件降价1元,超市平均每天可多售出10件.设每件商品降价![]() 元时,日盈利为
元时,日盈利为![]() 元.据此规律,解决下列问题:
元.据此规律,解决下列问题:
(1)降价后每件商品盈利 元,超市日销售量增加 件(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变的情况下,求每件商品降价多少元时,超市的日盈利最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com