
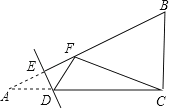
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为_____.
【答案】2或![]() 或
或![]() .
.
【解析】
由勾股定理求出AB,设AE=x,则EF=x,BF=10﹣2x;分三种情况讨论:
①当BF=BC时,列出方程,解方程即可;
②当BF=CF时,F在BC的垂直平分线上,得出AF=BF,列出方程,解方程即可;
③当CF=BC时,作CG⊥AB于G,则BG=FG![]() BF,由射影定理求出BG,再解方程即可.
BF,由射影定理求出BG,再解方程即可.
由翻折变换的性质得:AE=EF.
∵∠ACB=90°,AC=8,BC=6,
∴AB![]() 10.
10.
设AE=x,则EF=x,BF=10﹣2x.
分三种情况讨论:
①当BF=BC时,10﹣2x=6,
解得:x=2,
∴AE=2;
②当BF=CF时.
∵BF=CF,
∴∠B=∠FCB.
∵∠A+∠B=90°,∠FCA+∠FCB=90°,
∴∠A=∠FCA,
∴AF= FC.
∵BF=FC,
∴AF=BF,
∴x+x=10﹣2x,
解得:x![]() ,
,
∴AE![]() ;
;
③当CF=BC时,作CG⊥AB于G,如图所示:
则BG=FG![]() BF.
BF.
根据射影定理得:BC2=BGAB,
∴BG![]() ,
,
即![]() (10﹣2x)
(10﹣2x)![]() ,
,
解得:x![]() ,
,
∴AE![]() ;
;
综上所述:当△BCF为等腰三角形时,AE的长为:2或![]() 或
或![]() .
.
故答案为:2或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
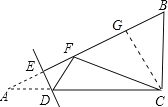
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行,组委会为了做好运动员的保障工作,沿途设置了4个补给站,分别是:A(粤东农批)、B(奥体中心)、C(球王故里)和D(滨江中路),志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务,每个补给站被选择的可能性相同.
(1)小明选择补给站C(球王故里)的概率是多少?
(2)用树状图或列表的方法,求小明和小红恰好选择同一个补给站的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
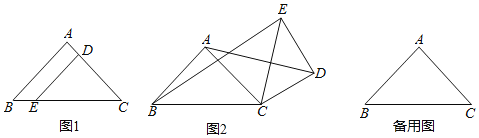
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:如图1,昌平南环大桥是经典的悬索桥,当今大跨度桥梁大多采用此种结构.此种桥梁各结构的名称如图2所示,其建造原理是在两边高大的桥塔之间,悬挂着主索,再以相应的间隔,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,主索几何形态近似符合抛物线.

图1
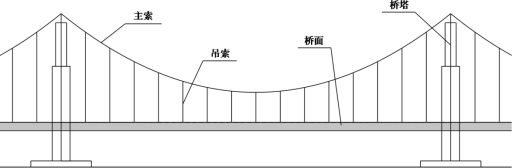
图2
材料2:如图3,某一同类型悬索桥,两桥塔AD=BC=10 m,间距AB为32 m,桥面AB水平,主索最低点为点P,点P距离桥面为2 m;

图3
为了进行研究,甲、乙、丙三位同学分别以不同方式建立了平面直角坐标系,如下图:
甲同学:以DC中点为原点,DC所在直线为x轴,建立平面直角坐标系;

乙同学:以AB中点为原点,AB所在直线为x轴,建立平面直角坐标系;

丙同学:以点P为原点,平行于AB的直线为x轴,建立平面直角坐标系.
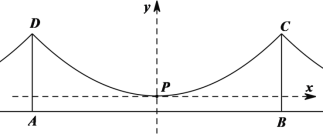
(1)请你选用其中一位同学建立的平面直角坐标系,写出此种情况下点C的坐标,并求出主索抛物线的表达式;
(2)距离点P水平距离为4 m和8 m处的吊索共四条需要更换,则四根吊索总长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种书包,平均每天可销售100件,每件盈利30元.试营销阶段发现:该商品每件降价1元,超市平均每天可多售出10件.设每件商品降价![]() 元时,日盈利为
元时,日盈利为![]() 元.据此规律,解决下列问题:
元.据此规律,解决下列问题:
(1)降价后每件商品盈利 元,超市日销售量增加 件(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变的情况下,求每件商品降价多少元时,超市的日盈利最大?最大为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com