
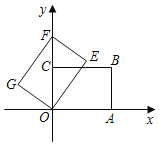
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A��C���������ϣ���A������Ϊ(4��0)����C������Ϊ(0��3)��������OABC�Ƶ�O��ʱ����ת�õ�����OEFG����B�Ķ�Ӧ��Fǡ������y���������ϣ�������OEFG��y������ƽ�ƣ�����E����x����ʱ���˶�ֹͣ����ƽ�Ƶľ���Ϊm���������ص����ΪS��
��1�����E�����ꣻ
��2����S��m�ĺ�����ϵʽ����ֱ��д��m��ȡֵ��Χ��
���𰸡���1����E������![]() ����2��S��
����2��S��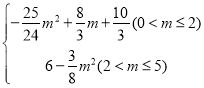
��������
��1����E��EH��x����H��������֪�����õ�OA��4��OC��3��������ת�����ʵõ�OE��OA��4��EF��OC��3�����ݹ��ɶ������ɵõ����ۣ�
��2��������������ۼ��ɣ�
�⣺��1����E��EH��x����H��
�ߵ�A������Ϊ��4��0������C������Ϊ��0��3����
��OA��4��OC��3��
�߽�����OABC�Ƶ�O��ʱ����ת�õ�����OEFG��
��OE��OA��4��EF��OC��3��
��OF��![]() ��5��
��5��
��EH��![]() ��
��![]() ��
��
��OH��![]() ��
��![]() ��
��![]() ��
��
���E�����꣺![]() ��
��
��2����ͼ2����![]() ��BC�Ϸ�ʱ����m
��BC�Ϸ�ʱ����m![]() ʱ��
ʱ��
![]() ��
��
��![]()
��![]()
��![]()
��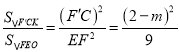 ��
��
��![]() ��
��
ͬ���ɵó���
![]() ��
��
��![]() ��
��
��ͼ��3����![]() ���߶�CO��ʱ����
���߶�CO��ʱ����![]() ʱ��
ʱ��
��![]() ��
��
��![]() ��
��
��S=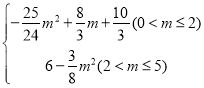 ��
��





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�������ƽ��ÿ�������100����ÿ��ӯ��30Ԫ.��Ӫ���η��֣�����Ʒÿ������1Ԫ������ƽ��ÿ��ɶ��۳�10��.��ÿ����Ʒ����![]() Ԫʱ����ӯ��Ϊ
Ԫʱ����ӯ��Ϊ![]() Ԫ.�ݴ˹��ɣ�����������⣺
Ԫ.�ݴ˹��ɣ�����������⣺
��1�����ۺ�ÿ����Ʒӯ�� Ԫ������������������ �����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������������£���ÿ����Ʒ���۶���Ԫʱ�����е���ӯ��������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��̳�����ij�ֱ��䣬ÿ̨����Ϊ2500Ԫ�����ۼ�Ϊ2900Ԫ��ƽ��ÿ�����۳�8̨�����鷢�֣������ۼ�ÿ����50Ԫ��ƽ��ÿ����ܶ��۳�4̨���̳�Ҫ��ʹ���ֱ������������ƽ��ÿ��ﵽ5000Ԫ��ÿ̨����Ӧ�ý��۶���Ԫ������ÿ̨���併��xԪ������������з��̣�������
A. (2900-x)(8+4��![]() )=5000 B. (400-x)(8+4��
)=5000 B. (400-x)(8+4��![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����2k+1��x+k2+1��0��
��1������������������ȵ�ʵ��������k��ȡֵ��Χ��
��2�������̵�����ǡ����һ���������ڱߵij�����k��2����þ��εĶԽ���L�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AB�ǡ�Oֱ������ACB��ƽ���߽���O��D����AC��m��BC��n����CD�ij�Ϊ_____���ú�m��n�Ĵ���ʽ��ʾ����
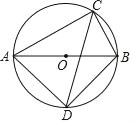
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ��Լһֱ���л�����Ĵ�ͳ���£�ij��ѧУ��ί���ԡ��ڼ��Լ��Ϊ���չһ���ݽ�������Ϊ���ȶ�ͬѧ��ÿ���㻨Ǯ���������һЩ�˽⣬��������˱�У����ͬѧ�����ݵ����������Ƴ������������в�������ͳ��ͼ����
��� | ���飨��λ��Ԫ�� | ���� |
A | 0��x��30 | 4 |
B | 30��x��60 | a |
C | 60��x��90 | b |
D | 90��x��120 | 8 |
E | 120��x��150 | 2 |
��������ͼ��������������⣺
��1����գ���ε����ͬѧ������ ���ˣ�a+b���� ����m���� ����
��2��������ͳ��ͼ������B��Բ�ĽǵĶ�����
��3����У����1200��ѧ���������ÿ���㻨Ǯ��������60��x��90��Χ��������
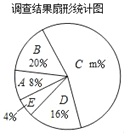
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ADC�У���ADC��90������DCΪֱ������Բ��O������AC�ڵ�F����B��CD���ӳ����ϣ�����BF����AD�ڵ�E����BED��2��C��
��1����֤��BF�ǡ�O�����ߣ�
��2����BF��FC��![]() �����O�İ뾶��
�����O�İ뾶��
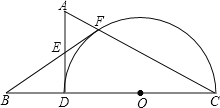
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ÿ�ܶ��������������ο�ǰ���ιۣ�����ο��࣬�Թ��е����������������Ӱ�죬��ͬʱ���ǵ���������ɺͱ���������⣬��Ҫ��֤һ������Ʊ���룬��ˣ�����ݲ�ȡ���Ǹ���Ʊ�۸�ķ��������Ʋι��������ڸ÷���ʵʩ�����з��֣�ÿ�ܲι�������Ʊ��֮���������ͼ��ʾ��һ�κ�����ϵ������������£����Ҫ��֤ÿ��![]() ��Ԫ����Ʊ���룬��ôÿ��Ӧ���ι������Ƕ��٣���Ʊ�۸�Ӧ�Ƕ��٣�
��Ԫ����Ʊ���룬��ôÿ��Ӧ���ι������Ƕ��٣���Ʊ�۸�Ӧ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC��y�ᣬBC��OA����A����C�ֱ���x�ᡢy����������ϣ�D���߶�BC��һ�㣬BD��![]() OA��2��AB��3����OAB��45����E��F�ֱ����߶�OA��AB�ϵ������㣬��ʼ�ձ��֡�DEF��45��������AEF��һ���߷��ۣ�����ǰ��������������ɵ��ı���Ϊ���Σ����߶�OE��ֵΪ_____��
OA��2��AB��3����OAB��45����E��F�ֱ����߶�OA��AB�ϵ������㣬��ʼ�ձ��֡�DEF��45��������AEF��һ���߷��ۣ�����ǰ��������������ɵ��ı���Ϊ���Σ����߶�OE��ֵΪ_____��
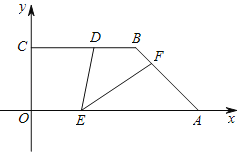
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com