
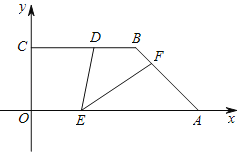
【题目】如图,BC⊥y轴,BC<OA,点A、点C分别在x轴、y轴的正半轴上,D是线段BC上一点,BD=![]() OA=2,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为_____.
OA=2,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°,将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为_____.
【答案】6﹣![]() 或6或9﹣3
或6或9﹣3![]()
【解析】
可得到∠DOE=∠EAF,∠OED=∠AFE,即可判定△DOE∽△EAF,分情况进行讨论:①当EF=AF时,△AEF沿AE翻折,所得四边形为菱形,进而得到OE的长;②当AE=AF时,△AEF沿EF翻折,所得四边形为菱形,进而得到OE的长;③当AE=EF时,△AEF沿AF翻折,所得四边形为菱形,进而得到OE的长.
解:连接OD,过点BH⊥x轴,
①沿着EA翻折,如图1:∵∠OAB=45°,AB=3,
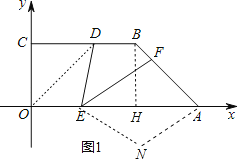
∴AH=BH=ABsin45°=![]() ,
,
∴CO=![]() ,
,
∵BD=![]() OA=2,
OA=2,
∴BD=2,OA=8,
∴BC=8﹣![]() ,
,
∴CD=6﹣![]() ;
;
∵四边形FENA是菱形,
∴∠FAN=90°,
∴四边形EFAN是正方形,
∴△AEF是等腰直角三角形,
∵∠DEF=45°,
∴DE⊥OA,
∴OE=CD=6﹣![]() ;
;
②沿着AF翻折,如图2:
∴AE=EF,
∴B与F重合,
∴∠BDE=45°,
∵四边形ABDE是平行四边形
∴AE=BD=2,
∴OE=OA﹣AE=8﹣2=6;
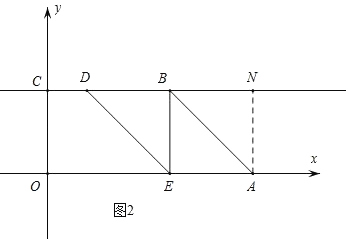
③沿着EF翻折,如图3:

∴AE=AF,
∵∠EAF=45°,
∴△AEF是等腰三角形,
过点F作FM⊥x轴,过点D作DN⊥x轴,
∴△EFM∽△DNE,
∴![]() ,
,
∴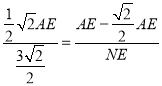 ,
,
∴NE=3﹣![]() ,
,
∴OE=6﹣![]() +3﹣
+3﹣![]() =9﹣3
=9﹣3![]() ;
;
综上所述:OE的长为6﹣![]() 或6或9﹣3
或6或9﹣3![]() ,
,
故答案为6﹣![]() 或6或9﹣3
或6或9﹣3![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
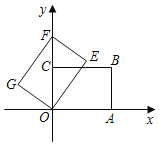
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A、C在坐标轴上,点A的坐标为(4,0).点C的坐标为(0,3).将矩形OABC绕点O逆时针旋转得到矩形OEFG,点B的对应点F恰好落在y轴正半轴上.将矩形OEFG沿y轴向下平移,当点E到达x轴上时,运动停止.设平移的距离为m,两矩形重叠面积为S.
(1)求点E的坐标;
(2)求S与m的函数关系式,并直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
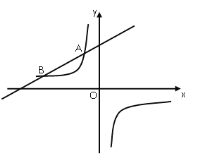
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
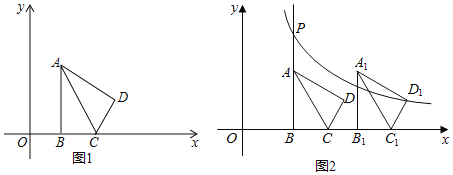
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
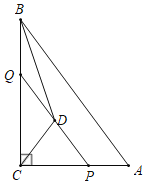
【题目】如图,在Rt△ABC中,∠C=90°,点P是边AC上一点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,BD平分∠ABC,以下四个结论①△BQD是等腰三角形;②BQ=DP;③PA=![]() QP;④
QP;④![]() =(1+
=(1+![]() )2;其中正确的结论的个数( )
)2;其中正确的结论的个数( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com