
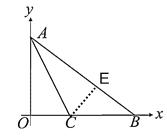
【题目】如图,在![]() 中,
中,![]() 是原点,
是原点,![]() (0,3),
(0,3),![]() (4,0),
(4,0),![]() 是
是![]() 的角平分线.
的角平分线.

(1)确定![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)在线段![]() 上是否有一点
上是否有一点![]() ,使点
,使点![]() 到
到![]() 轴和
轴和![]() 轴的距离相等,若存在,求出点
轴的距离相等,若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)在线段![]() 上是否有一点
上是否有一点![]() ,使
,使![]() 是等腰三角形,若存在,直接写出 点
是等腰三角形,若存在,直接写出 点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)直线AB的解析式为:![]() ;(2)点
;(2)点![]() 的坐标为(1,1);(3)点Q的坐标为:(
的坐标为(1,1);(3)点Q的坐标为:(![]() ,
,![]() ).
).
【解析】
(1)直接利用待定系数法求解即可;
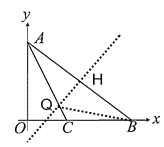
(2)过点C作CE⊥AB,设OC=CE=x,则BC=4-x,求出BE=2,然后在Rt△BCE中,利用勾股定理构建方程求出OC得到C点坐标,求出直线AC的解析式,联立直线AC的解析式和y=x,求出交点坐标即可;
(3)作线段AB的垂直平分线QH交AC于Q,交AB与H,设出直线QH的解析式,求出点H的坐标,代入可得直线QH的解析式,联立直线QH与直线AC的解析式,求出交点坐标即可.
解:(1)设直线AB的解析式为:y=kx+b,
代入A(0,3),B(4,0)得:![]() ,
,
解得: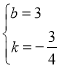 ,
,
∴直线AB的解析式为:![]() ;
;
(2)过点C作CE⊥AB,
∵AC平分∠OAB,
∴OC=CE,
∴设OC=CE=x,则BC=4-x,
易证△AOC≌△ACE,则AE=OA=3,
∵AB![]() ,
,
∴BE=5-3=2,
在Rt△BCE中,CE2+BE2=BC2,即x2+22=(4-x)2,
解得:![]() ,
,
∴C(![]() ,0),
,0),
设直线AC的解析式为:y=mx+n,
代入A(0,3),C(![]() ,0)得:
,0)得: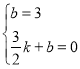 ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=-2x+3,
∵点![]() 在线段
在线段![]() 上,且到
上,且到![]() 轴和
轴和![]() 轴的距离相等,
轴的距离相等,
∴点P在直线y=x上,
联立![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为(1,1);
的坐标为(1,1);
(3)∵点Q在线段AC上,△AQB是等腰三角形,
∴如果存在,只有AQ=BQ一种情况,
作线段AB的垂直平分线QH交AC于Q,交AB与H,
∵直线AB的解析式为:![]() ,
,
∴ 设直线QH的解析式为:![]() ,
,
∵A(0,3),B(4,0),
∴H(2,![]() ),
),
将点H(2,![]() )代入
)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴直线QH的解析式为:![]() ,
,
联立直线QH与直线AC解析式得: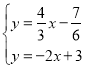 ,
,
解得:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角(即∠α=∠β).如图,设桌面上只剩下白球A和6号球B,希望A球撞击桌边上C点后反弹,再击中B球.
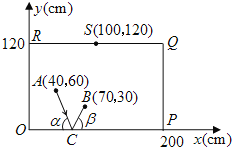
(1)在桌面上建立如图所示的坐标系,白球A(40,60)和6号球B(70,30),利用一次函数的知识,求出C点坐标;
(2)设桌边RQ上有球袋S(100,120),判定6号球被从C点反弹出的白球撞击后,能否落入球袋S中(假定6号球被撞击后的速度足够大),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在截面为半圆形的水槽内装有一些水,如图水面宽AB为6分米,如果再注入一些水后,水面上升1分米,此时水面宽度变为8分米。则该水槽截面半径为( )

A. 3分米 B. 4分米 C. 5分米 D. 10分米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-![]() x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0)
x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0)
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,记点M到线段BC的距离为d,当d取最大值时,求出此时M点的坐标;
(4)若点P是抛物线上一点,点E是直线y=-x+1上的动点,是否存在点P、E,使以点A,点B,点P,点E为顶点的四边形是平行四边形?若存在,请直接写出点E坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,点
,点![]() 在该函数的图象上,点
在该函数的图象上,点![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .设
.设![]() ,下列结论中:
,下列结论中:
①![]() 没有最大值;②
没有最大值;②![]() 没有最小值;③
没有最小值;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④满足![]() 的点
的点![]() 有四个.其中正确结论的个数有( )
有四个.其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若所求的二次函数图象与抛物线![]() 有相同的顶点,并且在对称轴的左侧,
有相同的顶点,并且在对称轴的左侧,![]() 随
随![]() 的增大而增大,在对称轴的右侧,
的增大而增大,在对称轴的右侧,![]() 随
随![]() 的增大而减小,则所求二次函数的解析式为( )
的增大而减小,则所求二次函数的解析式为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学住在同一小区,学校与小区相距2700米.一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图象.则( )

A.乙骑自行车的速度是180米/分B.乙到还车点时,甲,乙两人相距850米
C.自行车还车点距离学校300米D.乙到学校时,甲距离学校200米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com