练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数 (为常数),当自变量的值满足时,与其对应的函数值的最大值为-1,则的值为( )

    A. 3或6 B. 1或6 C. 1或3 D. 4或6

    【答案】B

    【解析】分h＜2、2≤h≤5和h＞5三种情况考虑：当h＜2时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论；当2≤h≤5时，由此时函数的最大值为0与题意不符，可得出该情况不存在；当h＞5时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论．综上即可得出结论．

    如图，

    当h＜2时，有-（2-h）2=-1，

    解得：h1=1，h2=3（舍去）；

    当2≤h≤5时，y=-（x-h）2的最大值为0，不符合题意；

    当h＞5时，有-（5-h）2=-1，

    解得：h3=4（舍去），h4=6．

    综上所述：h的值为1或6．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交点C，抛物线过A，C两点，与x轴交于另一点B．

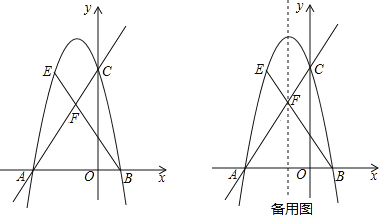
    （1）求抛物线的解析式．

    （2）在直线AC上方的抛物线上有一动点E，连接BE，与直线AC相交于点F，当时，求的值．

    （3）点N是抛物线对称轴上一点，在（2）的条件下，若点E位于对称轴左侧，在抛物线上是否存在一点M，使以M，N，E，B为顶点的四边形是平行四边形？若存在，直接写出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．

    (1) 求一次函数解析式；

    (2)求顶点P的坐标；

    (3)平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且，求点M坐标；

    (4)设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两个种子店都销售“黄金1号”玉米种子．在甲店，该种子的价格为 5元 / kg，如果一次购买2 kg 以上的种子，超过 2 kg 部分的种子的价格打8折．在乙店，不论一次购买该种子的数量是多少，价格均为4.5 元 / kg．

    （1）根据题意，填写下表：

    （2）设一次购买种子的数量为 kg（）. 在甲店购买的付款金额记为元，在乙店购买的付款金额为元，分别求，关于的函数解析式；

    （3） 若在同一店中一次购买种子的付款金额是36元，则最多可购买种子______ kg.若在同一店中一次购买种子10 kg，则最少付款金额是________元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：

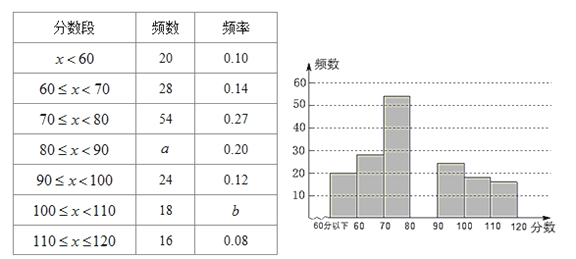
    请根据以上图表提供的信息，解答下列问题：

    （1）随机抽取部分学生的总人数是_________人，表格中的_________．

    （2）请补全频数分布直方图；

    （3）如果把成绩在90分以上(含90分)定为优秀，那么该市16000名九年级考生数学成绩为优秀的学生约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线L：y＝x2+bx+c经过点M（2，﹣3），与y轴交于点C（0，﹣3）．

    （1）求抛物线L的表达式；

    （2）试判断抛物线L与x轴交点的情况；

    （3）平移该抛物线，设平移后的抛物线为L′，抛物线L′的顶点记为P，它的对称轴与x轴交于点Q，已知点N（2，﹣8），怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

    （1）求甲、乙两种树苗每棵的价格各是多少元？

    （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，的网格中，均在格点上，请用无刻度的直尺作图（保留作图痕迹，不写作法）．

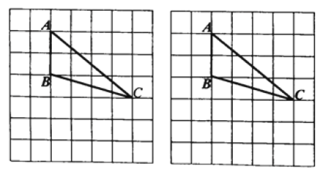
    （1）在图1中找一格点，使得为等腰三角形（找到一个即可）；

    （2）在图2中作出的角平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据报载，在“百万家庭低碳行，垃圾分类要先行”活动中，某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查，并将调查结果分别绘成条形图（图1）、扇形图（图2）．

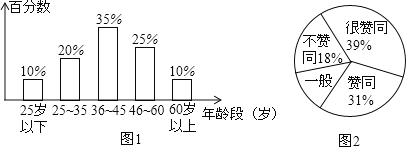
    （1）图2中所缺少的百分数是_________；

    （2）这次随机调查中，如果公民年龄的中位数是正整数，那么这个中位数所在年龄段是_________（填写年龄段）；

    （3）这次随机调查中，年龄段是“25岁以下”的公民中“不赞成”的有5名，它占“25岁以下”人数的百分数是________；

    （4）如果把所持态度中的“很赞同”和“赞同”统称为“支持”，那么这次被调查公民中“支持”的人有_______名．

    查看答案和解析>>

    同步练习册答案