
【题目】已知抛物线L:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).
(1)求抛物线L的表达式;
(2)试判断抛物线L与x轴交点的情况;
(3)平移该抛物线,设平移后的抛物线为L′,抛物线L′的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?
【答案】(1)y=x2﹣2x﹣3;(2)抛物线L与x轴有两个不同的交点;(3)将原抛物线先向左平移3个单位,再向下平移1个单位,可得到符合条件的抛物线L
【解析】
(1)将M、C两点的坐标代入y=-x2+bx+c,根据待定系数法即可解答;
(2)利用一元二次方程的根的判别式即可解答;
(3)先确定M(2,-3)、N(2,-8),则当PQ=MN=5时,四边形MNPQ为平行四边形.设点Q(m,0),则P点的坐标为(m,-5),根据菱形的性质得到PN=MN=5,故(m-2)2+(-5+8)2=52,即点P的坐标为(6,-5)或(-2,-5),最后就两个顶点分别根据平移规律解答即可.
解:(1)抛物线L:y=x2+bx+c经过点M(2,﹣3),点C(0,﹣3).
代入得![]() ,
,
解得![]() ,
,
∴抛物线L的表达式为:y=x2﹣2x﹣3;
(2)令x2﹣2x﹣3=0,则△=b2﹣4ac=(﹣2)2﹣4×1×(﹣3)=16>0,
∴抛物线L与x轴有两个不同的交点;
(3)由题意得,M(2,﹣3),N(2,﹣8),
∴MN∥y轴,MN=5,
∵PQ∥MN∥y轴,
∴当PQ=MN=5时,四边形MNPQ为平行四边形.
设点Q(m,0),则P点的坐标为(m,﹣5),
要使得以M、N、P、Q为顶点的四边形为菱形,
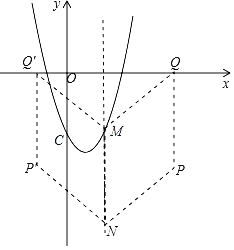
只需PN=MN=5,
∴(m﹣2)2+(﹣5+8)2=52,
解得m1=6,m2=﹣2,
∴点P的坐标为(6,﹣5)或(﹣2,﹣5).
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线L的顶点坐标为(1,﹣4),
∴①当点P的坐标为(6,﹣5)时,6﹣5=1,﹣5﹣(﹣4)=﹣1,
∴将原抛物线先向右平移5个单位,再向下平移1个单位,可得到符合条件的抛物线L′;
②当点P的坐标为(﹣2,﹣5)时,﹣2﹣1=﹣3,﹣5﹣(﹣4)=﹣1,
∴将原抛物线先向左平移3个单位,再向下平移1个单位,可得到符合条件的抛物线L″.


科目:初中数学 来源: 题型:
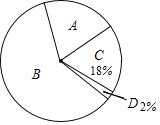
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
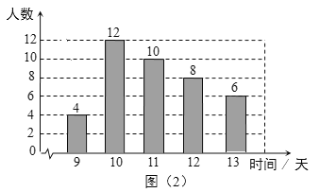
【题目】学校为了解全校学生参加社会实践活动情况,随机调查了部分学生一学期参加社会实践活动的时间(单位:天),并用得到的数据绘制了统计图(1)和图 (2). 请根据图中提供的信息,回答下列问题:

![]()
(1) 本次随机调查的学生人数是_______,图(1)中m的值是_______;
(2)求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数;
(3)该校有480名学生,根据获取的社会实践活动时间样本数据,估计该校一学期社会实践活动时间大于10 天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最大值为-1,则
的最大值为-1,则![]() 的值为( )
的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在四等分的圆形转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券(指针落在分界线上不计次数,需要再次转动转盘一次,直到指针没有落在分界线上),一个顾客刚好消费300元,并参加促销活动,转了2次转盘.
(1)请你用画树形图法或列表法,求出该顾客两次获得购物券金额和的所有可能结果;
(2)求出该顾客两次获得购物金额和不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
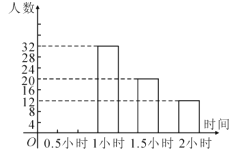
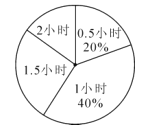
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图中两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)户外活动时间为0.5小时的人数是________,表示户外活动时间为2小时的扇形圆心角的度数是________并补全条形统计图;
(3)本次调查中学生参加户外活动的平均时间是否符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若干个半径为
中,若干个半径为![]() 个单位长度,圆心角是
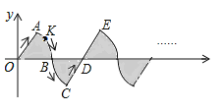
个单位长度,圆心角是![]() 扇形按图中的方式摆放,动点
扇形按图中的方式摆放,动点![]() 从原点
从原点![]() 出发,沿着“半径
出发,沿着“半径![]() 弧
弧![]() 弧
弧![]() 半径
半径![]() 半径
半径![]() ...”的曲线运动,若点
...”的曲线运动,若点![]() 在线段上运动的速度为每秒
在线段上运动的速度为每秒![]() 个单位长度,在弧线上运动的速度为每秒
个单位长度,在弧线上运动的速度为每秒![]() 个单位长度,设第
个单位长度,设第![]() 秒运动到点
秒运动到点![]() (
(![]() 为自然数),则
为自然数),则![]() 的坐标是___________________;
的坐标是___________________;![]() 的坐标是_____________________.
的坐标是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为![]() ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于![]() 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )

A. 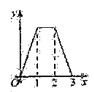 B.
B. 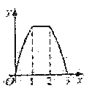 C.
C. 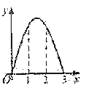 D.
D. 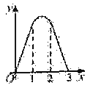
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com