
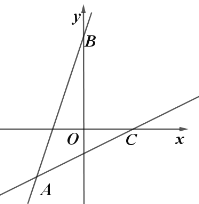
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,现将直线
,现将直线![]() 绕点
绕点![]() 顺时针方向旋转45°交
顺时针方向旋转45°交![]() 轴于点
轴于点![]() ,则直线
,则直线![]() 的函数表达式是_________.
的函数表达式是_________.
【答案】![]()
【解析】
过点C作![]() 交AB于点F,根据旋转
交AB于点F,根据旋转![]() 可得△FCA是等腰直角三角形,得到FC=AF,设C点的坐标为
可得△FCA是等腰直角三角形,得到FC=AF,设C点的坐标为![]() ,根据A,B的坐标可求出AB所在直线的解析式为
,根据A,B的坐标可求出AB所在直线的解析式为![]() ,根据直线垂直的特点可以求出FC所在的直线解析式为
,根据直线垂直的特点可以求出FC所在的直线解析式为![]() ,联立可得F的坐标为
,联立可得F的坐标为![]() ,根据勾股定理可得出FC和AF的值,然后联立式子可求出C点的坐标,进而求的解析式.
,根据勾股定理可得出FC和AF的值,然后联立式子可求出C点的坐标,进而求的解析式.
过点C作![]() 交AB于点F.
交AB于点F.
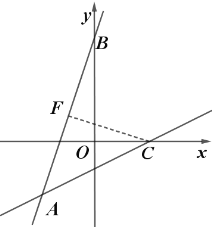
设直线AB所在的直线解析式为![]() ,由题可知
,由题可知![]() ,
,![]() ,得
,得
![]()
设直线CF所在直线的解析式为![]() ,
,![]()
∵直线AB与直线CF垂直
∴![]()
∴![]()
∴![]()
联立方程组得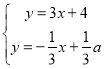
解得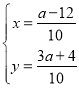
∴F ![]() ,根据题意可得
,根据题意可得
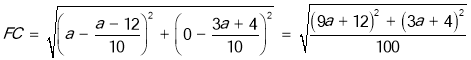
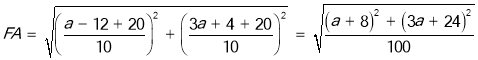
又∵![]()
∴△FCA是等腰直角三角形 ∴FC=FA 得到 整理可得 得到 解方程可得: 所以得到C点的坐标为 设AC所在直线的解析式为 把A,C代入可得 ∴直线AC的函数表达式为 故答案为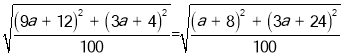
![]()
![]()
![]() (舍去)
(舍去)![]()
![]()
![]()
![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“购买![]() 张彩票就中奖”是不可能事件
张彩票就中奖”是不可能事件
B.“概率为![]() 的事件”是不可能事件
的事件”是不可能事件
C.“任意画一个六边形,它的内角和等于![]() ”是必然事件
”是必然事件
D.从![]() 中任取
中任取![]() 个不同的数,分别记为
个不同的数,分别记为![]() 和
和![]() ,那么
,那么![]() 的概率是
的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() (
(![]() )与
)与![]() 轴交于A、B两点(点B在A的右侧),与
轴交于A、B两点(点B在A的右侧),与![]() 轴交于点C,D是抛物线的顶点.
轴交于点C,D是抛物线的顶点.
(1)当![]() 时,求顶点D 的坐标
时,求顶点D 的坐标
(2)若OD = OB,求![]() 的值;
的值;
(3)设E为A,B两点间抛物线上的一个动点(含端点A,B),过点E作EH⊥![]() 轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为
轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个种子店都销售“黄金1号”玉米种子.在甲店,该种子的价格为 5元 / kg,如果一次购买2 kg 以上的种子,超过 2 kg 部分的种子的价格打8折.在乙店,不论一次购买该种子的数量是多少,价格均为4.5 元 / kg.
(1)根据题意,填写下表:

(2)设一次购买种子的数量为![]() kg(
kg(![]() ). 在甲店购买的付款金额记为
). 在甲店购买的付款金额记为![]() 元,在乙店购买的付款金额为
元,在乙店购买的付款金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3) 若在同一店中一次购买种子的付款金额是36元,则最多可购买种子______ kg.若在同一店中一次购买种子10 kg,则最少付款金额是________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
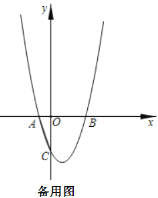
【题目】已知,在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]()
![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的侧),与
的侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求![]() 的值;
的值;

(2)如图2,![]() 是
是![]() 轴上一点(不与点
轴上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
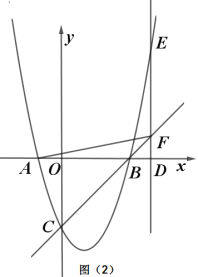
①当点![]() 在点
在点![]() 右侧时,连接AF,当
右侧时,连接AF,当![]() 时,求
时,求![]() 的长.
的长.
②当点![]() 在运动时,若
在运动时,若![]() 、
、![]() 、
、![]() 中有两条线段相等,此时点
中有两条线段相等,此时点![]() 的坐标_________.
的坐标_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).
(1)求抛物线L的表达式;
(2)试判断抛物线L与x轴交点的情况;
(3)平移该抛物线,设平移后的抛物线为L′,抛物线L′的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
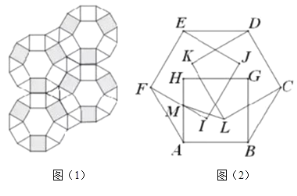
【题目】建筑工人用边长相等的正六边形、正方形、正三角形三种瓷砖铺设地面,正方形瓷砖分黑白两种颜色,密铺成图(1)的形状.用水泥浇筑前,为方便施工,工人要先把瓷砖按图1方式先摆放好,一工人摆放时,无意间将3块黑色正方形瓷砖上翻到一个正六边形的上面,其中三个正方形的一条边分别和正六边形的三条边重合,如图(2)所示.按图(2)方式给各点作上标注,若正方形的边长![]() ,则
,则![]() _____
_____![]() (不考虑瓷砖的厚度)
(不考虑瓷砖的厚度)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com