
【题目】某商场为了吸引顾客,设计了一种促销活动:在四等分的圆形转盘上依次标有“0元”、“10元”、“30元”、“50元”字样,购物每满300元可以转动转盘2次,每次转盘停下后,顾客可以获得指针所指区域相应金额的购物券(指针落在分界线上不计次数,需要再次转动转盘一次,直到指针没有落在分界线上),一个顾客刚好消费300元,并参加促销活动,转了2次转盘.
(1)请你用画树形图法或列表法,求出该顾客两次获得购物券金额和的所有可能结果;
(2)求出该顾客两次获得购物金额和不低于50元的概率.
科目:初中数学 来源: 题型:
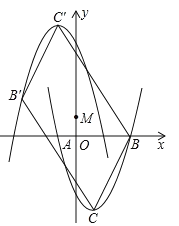
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于A(﹣1,0),B(3,0)两点,点C为抛物线的顶点.点M(0,m)为y轴上的动点,将抛物线绕点M旋转180°,得到新的抛物线,其中B、C旋转后的对应点分别记为B'、C'.
(1)若a=1,求原抛物线的函数表达式;
(2)在(1)条件下,当四边形BCB'C'的面积为40时,求m的值;
(3)探究a满足什么条件时,存在点M,使得四边形BCB'C'为菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() (
(![]() )与
)与![]() 轴交于A、B两点(点B在A的右侧),与
轴交于A、B两点(点B在A的右侧),与![]() 轴交于点C,D是抛物线的顶点.
轴交于点C,D是抛物线的顶点.
(1)当![]() 时,求顶点D 的坐标
时,求顶点D 的坐标
(2)若OD = OB,求![]() 的值;
的值;
(3)设E为A,B两点间抛物线上的一个动点(含端点A,B),过点E作EH⊥![]() 轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为
轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]()
![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的侧),与
的侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
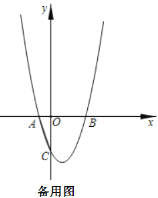
(1)如图1,求![]() 的值;
的值;

(2)如图2,![]() 是
是![]() 轴上一点(不与点
轴上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
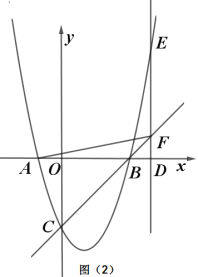
①当点![]() 在点
在点![]() 右侧时,连接AF,当
右侧时,连接AF,当![]() 时,求
时,求![]() 的长.
的长.
②当点![]() 在运动时,若
在运动时,若![]() 、
、![]() 、
、![]() 中有两条线段相等,此时点
中有两条线段相等,此时点![]() 的坐标_________.
的坐标_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).
(1)求抛物线L的表达式;
(2)试判断抛物线L与x轴交点的情况;
(3)平移该抛物线,设平移后的抛物线为L′,抛物线L′的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
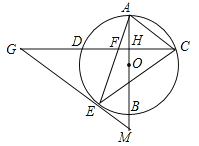
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
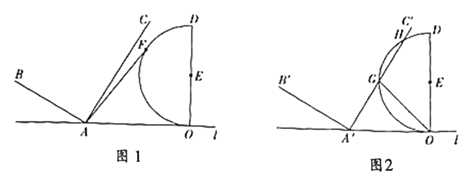
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com