
ЁОЬтФПЁПОнБЈдиЃЌдкЁААйЭђМвЭЅЕЭЬМааЃЌРЌЛјЗжРрвЊЯШааЁБЛюЖЏжаЃЌФГЕиЧјЖдЫцЛњГщШЁЕФ1000УћЙЋУёЕФФъСфЖЮЗжВМЧщПіКЭЖдРЌЛјЗжРрЫљГжЬЌЖШНјааЕїВщЃЌВЂНЋЕїВщНсЙћЗжБ№ЛцГЩЬѕаЮЭМЃЈЭМ1ЃЉЁЂЩШаЮЭМЃЈЭМ2ЃЉЃЎ
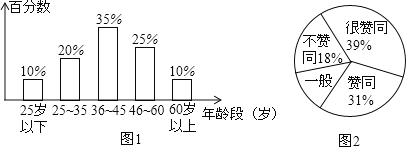
ЃЈ1ЃЉЭМ2жаЫљШБЩйЕФАйЗжЪ§ЪЧ_________ЃЛ
ЃЈ2ЃЉетДЮЫцЛњЕїВщжаЃЌШчЙћЙЋУёФъСфЕФжаЮЛЪ§ЪЧе§ећЪ§ЃЌФЧУДетИіжаЮЛЪ§ЫљдкФъСфЖЮЪЧ_________ЃЈЬюаДФъСфЖЮЃЉЃЛ
ЃЈ3ЃЉетДЮЫцЛњЕїВщжаЃЌФъСфЖЮЪЧЁА25ЫъвдЯТЁБЕФЙЋУёжаЁАВЛдоГЩЁБЕФга5УћЃЌЫќеМЁА25ЫъвдЯТЁБШЫЪ§ЕФАйЗжЪ§ЪЧ________ЃЛ
ЃЈ4ЃЉШчЙћАбЫљГжЬЌЖШжаЕФЁАКмдоЭЌЁБКЭЁАдоЭЌЁБЭГГЦЮЊЁАжЇГжЁБЃЌФЧУДетДЮБЛЕїВщЙЋУёжаЁАжЇГжЁБЕФШЫга_______УћЃЎ
ЁОД№АИЁП(1) 12%ЃЌ (2) 36~45ЃЌ (3) 5%ЃЌ (4) 700ШЫЁЃ
ЁОНтЮіЁП
ЃЈ1ЃЉБОЬташЯШИљОнвбжЊЬѕМўЃЌдйНсКЯЭМаЮСаГіЪНзгЃЌНтГіНсЙћМДПЩЃЎ
ЃЈ2ЃЉБОЬташЯШИљОнжаЮЛЪ§ЕФИХФюМДПЩЕУГіД№АИЃЎ
ЃЈ3ЃЉБОЬташЯШЧѓГі25ЫъвдЯТЕФзмШЫЪ§ЃЌдйгУ5Г§вдзмШЫЪ§МДПЩЕУГіД№АИЃЎ
ЃЈ4ЃЉБОЬташЯШЧѓГіетДЮБЛЕїВщЙЋУёжажЇГжЕФШЫЫљеМЕФАйЗжБШЃЌдйГЫвдзмШЫЪ§МДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉЭМ2жаЫљШБЩйЕФАйЗжЪ§ЪЧЃК1Љ39%Љ18%Љ31%=12%ЃЛ
ЃЈ2ЃЉЁпЙВ1000УћЙЋУёЃЌ
ЁретИіжаЮЛЪ§ЫљдкФъСфЖЮЪЧЕк500КЭЕк501ИіЪ§ЕФЦНОљЪ§ЃЌ
ЁретИіжаЮЛЪ§ЫљдкФъСфЖЮЪЧЃК36ЁЋ45ЫъЃЛ
ЃЈ3ЃЉЁпФъСфЖЮЪЧЁА25ЫъвдЯТЁБЕФЙЋУёжаЁАВЛдоГЩЁБЕФга5УћЃЌ
ЁА25ЫъвдЯТЁБЕФШЫЪ§ЪЧ1000ЁС10%ЃЌ
ЁрЫќеМЁА25ЫъвдЯТЁБШЫЪ§ЕФАйЗжЪ§ЪЧ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЁпЫљГжЬЌЖШжаЁАКмдоЭЌЁБКЭЁАдоЭЌЁБЕФШЫЪ§ЫљеМЕФАйЗжБШЗжБ№ЪЧЃЛ39%ЃЌ31%ЃЌ
ЁретДЮБЛЕїВщЙЋУёжаЁАжЇГжЁБЕФШЫга1000ЁСЃЈ39%+31%ЃЉ=700ЃЈШЫЃЉЃЌ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() (
(![]() ЮЊГЃЪ§),ЕБздБфСП
ЮЊГЃЪ§),ЕБздБфСП![]() ЕФжЕТњзу
ЕФжЕТњзу![]() ЪБ,гыЦфЖдгІЕФКЏЪ§жЕ
ЪБ,гыЦфЖдгІЕФКЏЪ§жЕ![]() ЕФзюДѓжЕЮЊ-1,дђ
ЕФзюДѓжЕЮЊ-1,дђ![]() ЕФжЕЮЊ( )
ЕФжЕЮЊ( )
A. 3Лђ6 B. 1Лђ6 C. 1Лђ3 D. 4Лђ6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
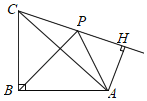
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧШ§НЧаЮABCжаЃЌЁЯABCЃН90ЁуЃЌBAЃНBCЃЌНЋBCШЦЕуBЫГЪБеыа§зЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЃЌЕУЕНBPЃЌСЌНсCPЃЌЙ§ЕуAзїAHЁЭCPНЛCPЕФбгГЄЯпгкЕуHЃЌСЌНсAPЃЌдђЁЯPAHЕФЖШЪ§ЃЈЁЁЁЁЃЉ
A.ЫцзХІШЕФдіДѓЖјдіДѓ
B.ЫцзХІШЕФдіДѓЖјМѕаЁ
C.ВЛБф
D.ЫцзХІШЕФдіДѓЃЌЯШдіДѓКѓМѕаЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() (
(![]() )ЃЎ
)ЃЎ
ЃЈ1ЃЉЙлВьВТЯы
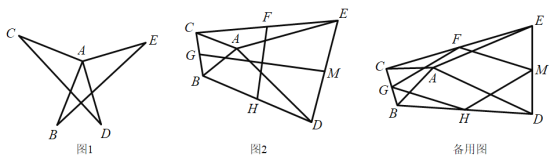
ШчЭМ1ЃЌЕБ![]() ЪБЃЌЧыжБНгаДГіЯпЖЮ
ЪБЃЌЧыжБНгаДГіЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃКЁЁЁЁЁЁЁЁЃЛЮЛжУЙиЯЕЃКЁЁЁЁЁЁЁЁЃЛ
ЕФЪ§СПЙиЯЕЃКЁЁЁЁЁЁЁЁЃЛЮЛжУЙиЯЕЃКЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌаДГі
ЕФжаЕуЃЌаДГі![]() гы
гы![]() ЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉНтОіЮЪЬт
ШчЭМЃЌвбжЊЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌжБНгаДГіЫФБпаЮ
а§зЊЃЌжБНгаДГіЫФБпаЮ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЕФЗЖЮЇ(гУКЌ
ЕФЗЖЮЇ(гУКЌ![]() ЕФШ§НЧКЏЪ§ЪНзгБэЪО)ЃЎ
ЕФШ§НЧКЏЪ§ЪНзгБэЪО)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
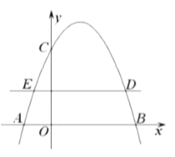
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌНЛХзЮяЯпгк
ЃЌНЛХзЮяЯпгк![]() ЁЂ
ЁЂ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЃЌ
ЃЌ![]() СНЕуЕФзјБъЃЛ
СНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЪБЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЗНГЬ
ЪБЃЌЗНГЬ![]() дк
дк![]() ЕФЗЖЮЇФкгаЪЕЪ§НтЃЌЧыжБНгаДГі
ЕФЗЖЮЇФкгаЪЕЪ§НтЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃКЁЁЁЁЁЁЁЁЃЎ
ЕФШЁжЕЗЖЮЇЃКЁЁЁЁЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() ЖМгыжБЯпlДЙжБЃЌДЙзуЗжБ№ЮЊMЃЌNЃЌMN=1ЃЌе§ЗНаЮABCDЕФБпГЄЮЊ
ЖМгыжБЯпlДЙжБЃЌДЙзуЗжБ№ЮЊMЃЌNЃЌMN=1ЃЌе§ЗНаЮABCDЕФБпГЄЮЊ![]() ЃЌЖдНЧЯпACдкжБЯпlЩЯЃЌЧвЕуCЮЛгкЕуMДІЃЌНЋе§ЗНаЮABCDбиlЯђгвЦНвЦЃЌжБЕНЕуAгыЕуNжиКЯЮЊжЙЃЌМЧЕуCЦНвЦЕФОрРыЮЊxЃЌе§ЗНаЮABCDЕФБпЮЛгк
ЃЌЖдНЧЯпACдкжБЯпlЩЯЃЌЧвЕуCЮЛгкЕуMДІЃЌНЋе§ЗНаЮABCDбиlЯђгвЦНвЦЃЌжБЕНЕуAгыЕуNжиКЯЮЊжЙЃЌМЧЕуCЦНвЦЕФОрРыЮЊxЃЌе§ЗНаЮABCDЕФБпЮЛгк![]() жЎМфВПЗжЕФГЄЖШКЭЮЊyЃЌдђyЙигкxЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈ ЃЉ
жЎМфВПЗжЕФГЄЖШКЭЮЊyЃЌдђyЙигкxЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈ ЃЉ

A. 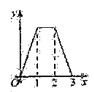 B.
B. 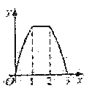 C.
C. 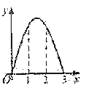 D.
D. 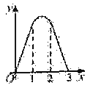
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЗўзАЙЋЫОеаЙЄЙуИцГаХЕЃКЪьСЗЙЄШЫУПдТЙЄзЪжСЩй3000дЊЃЎУПЬьЙЄзї8аЁЪБЃЌвЛИідТЙЄзї25ЬьЃЎдТЙЄзЪЕзаН800дЊЃЌСэМгМЦМўЙЄзЪЃЎМгЙЄ1МўAаЭЗўзАМЦГъ16дЊЃЌМгЙЄ1МўBаЭЗўзАМЦГъ12дЊЃЎдкЙЄзїжаЗЂЯжвЛУћЪьСЗЙЄМгЙЄ1МўAаЭЗўзАКЭ2МўBаЭЗўзАаш4аЁЪБЃЌМгЙЄ3МўAаЭЗўзАКЭ1МўBаЭЗўзАаш7аЁЪБЃЎЃЈЙЄШЫдТЙЄзЪ=ЕзаН+МЦМўЙЄзЪЃЉ
ЃЈ1ЃЉвЛУћЪьСЗЙЄМгЙЄ1МўAаЭЗўзАКЭ1МўBаЭЗўзАИїашвЊЖрЩйаЁЪБЃП
ЃЈ2ЃЉвЛЖЮЪБМфКѓЃЌЙЋЫОЙцЖЈЃКЁАУПУћЙЄШЫУПдТБиаыМгЙЄAЃЌBСНжжаЭКХЕФЗўзАЃЌЧвМгЙЄAаЭЗўзАЪ§СПВЛЩйгкBаЭЗўзАЕФвЛАыЁБЃЎЩшвЛУћЪьСЗЙЄШЫУПдТМгЙЄAаЭЗўзАaМўЃЌЙЄзЪзмЖюЮЊWдЊЃЎЧыФудЫгУЫљбЇжЊЪЖХаЖЯИУЙЋЫОдкжДааЙцЖЈКѓЪЧЗёЮЅБГСЫЙуИцГаХЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
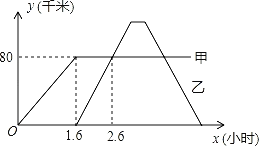
ЁОЬтФПЁПAЃЌBСНЕиЯрОр200ЧЇУзЃЎдчЩЯ8ЃК00ЛѕГЕМзДгAЕиГіЗЂНЋвЛХњЮязЪдЫЭљBЕиЃЌааЪЛвЛЖЮТЗГЬКѓГіЯжЙЪеЯЃЌМДПЬЭЃГЕгыBЕиСЊЯЕЃЎBЕиЪеЕНЯћЯЂКѓСЂМДХЩЛѕГЕввДгBЕиГіЗЂШЅНгдЫМзГЕЩЯЕФЮязЪЃЎЛѕГЕввгіЕНМзКѓЃЌгУСЫ18ЗжжгНЋЮязЪДгЛѕГЕМзАсдЫЕНЛѕГЕввЩЯЃЌЫцКѓПЊЭљBЕиЃЎСНСОЛѕГЕРыПЊИїздГіЗЂЕиЕФТЗГЬyЃЈЧЇУзЃЉгыЪБМфxЃЈаЁЪБЃЉЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎЃЈЭЈЛАЕШЦфЫћЪБМфКіТдВЛМЦЃЉ
ЃЈ1ЃЉЧѓЛѕГЕввдкгіЕНЛѕГЕМзЧАЃЌЫќРыПЊГіЗЂЕиЕФТЗГЬyЙигкxЕФКЏЪ§БэДяЪНЃЎ
ЃЈ2ЃЉвђЪЕМЪашвЊЃЌвЊЧѓЛѕГЕввЕНДяBЕиЕФЪБМфБШЛѕГЕМзАДдРДЕФЫйЖШе§ГЃЕНДяBЕиЕФЪБМфзюЖрЭэ1ИіаЁЪБЃЌЮЪЛѕГЕввЗЕЛиBЕиЕФЫйЖШжСЩйЮЊУПаЁЪБЖрЩйЧЇУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬсГі
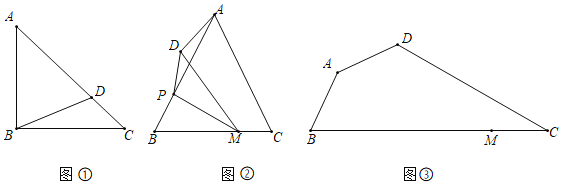
ЃЈ1ЃЉШчЭМЂйЃЌдкЕШбќRtЁїABCжаЃЌаББпACЃН4ЃЌЕуDЮЊACЩЯвЛЕуЃЌСЌНгBDЃЌдђBDЕФзюаЁжЕЮЊЁЁ ЁЁЃЛ
ЮЪЬтЬНОП
ЃЈ2ЃЉШчЭМЂкЃЌдкЁїABCжаЃЌABЃНACЃН5ЃЌBCЃН6ЃЌЕуMЪЧBCЩЯвЛЕуЃЌЧвBMЃН4ЃЌЕуPЪЧБпABЩЯвЛЖЏЕуЃЌСЌНгPMЃЌНЋЁїBPMбиPMЗелЕУЕНЁїDPMЃЌЕуDгыЕуBЖдгІЃЌСЌНгADЃЌЧѓADЕФзюаЁжЕЃЛ
ЮЪЬтНтОі
ЃЈ3ЃЉШчЭМЂлЃЌЫФБпаЮABCDЪЧЙцЛЎжаЕФанЯаЙуГЁЪОвтЭМЃЌЦфжаЁЯBADЃНЁЯADCЃН135ЁуЃЌЁЯDCBЃН30ЁуЃЌADЃН2![]() kmЃЌABЃН3kmЃЌЕуMЪЧBCЩЯвЛЕуЃЌMCЃН4kmЃЎЯжМЦЛЎдкЫФБпаЮABCDФкбЁШЁвЛЕуPЃЌАбЁїDCPНЈГЩЩЬвЕЛюЖЏЧјЃЌЦфгрВПЗжНЈГЩОАЙлТЬЛЏЧјЃЎЮЊЗНБуНјШыЩЬвЕЧјЃЌашаоНЈаЁТЗBPЁЂMPЃЌДгЪЕгУКЭУРЙлЕФНЧЖШЃЌвЊЧѓТњзуЁЯPMBЃНЁЯABPЃЌЧвОАЙлТЬЛЏЧјУцЛ§зуЙЛДѓЃЌМДЁїDCPЧјгђУцЛ§ОЁПЩФмаЁЃЎдђдкЫФБпаЮABCDФкЪЧЗёДцдкетбљЕФЕуPЃПШєДцдкЃЌЧыЧѓГіЁїDCPУцЛ§ЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
kmЃЌABЃН3kmЃЌЕуMЪЧBCЩЯвЛЕуЃЌMCЃН4kmЃЎЯжМЦЛЎдкЫФБпаЮABCDФкбЁШЁвЛЕуPЃЌАбЁїDCPНЈГЩЩЬвЕЛюЖЏЧјЃЌЦфгрВПЗжНЈГЩОАЙлТЬЛЏЧјЃЎЮЊЗНБуНјШыЩЬвЕЧјЃЌашаоНЈаЁТЗBPЁЂMPЃЌДгЪЕгУКЭУРЙлЕФНЧЖШЃЌвЊЧѓТњзуЁЯPMBЃНЁЯABPЃЌЧвОАЙлТЬЛЏЧјУцЛ§зуЙЛДѓЃЌМДЁїDCPЧјгђУцЛ§ОЁПЩФмаЁЃЎдђдкЫФБпаЮABCDФкЪЧЗёДцдкетбљЕФЕуPЃПШєДцдкЃЌЧыЧѓГіЁїDCPУцЛ§ЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com