
 和菱形
和菱形 中,点
中,点 在同一条直线上,
在同一条直线上, 是线段
是线段 的中点,连结
的中点,连结 .探究
.探究 与
与 的位置关系及
的位置关系及 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长 交
交 于点
于点 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.
 ,写出线段
,写出线段 与
与 的位置关系及
的位置关系及 的值,并说明理由;
的值,并说明理由; 绕点
绕点 顺时针旋转,使菱形
顺时针旋转,使菱形 的对角线
的对角线 恰好与菱形
恰好与菱形 的边
的边 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明. ,将菱形
,将菱形 绕点
绕点 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出 的值(用含
的值(用含 的式子表示).
的式子表示). 与
与 的位置关系是 ;
的位置关系是 ; .
. 与
与 的位置关系是
的位置关系是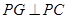 ,
, ;………………………………4分
;………………………………4分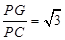 .……………………10分
.……………………10分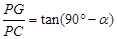 ………………………………………………………12分
………………………………………………………12分

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示): ;
; ,
, 的中点
的中点 ,
, ,连接
,连接 ;
; 为圆心,
为圆心, 长为半径画弧,交
长为半径画弧,交 的延长线于
的延长线于 ;
; 作
作 ⊥
⊥ ,交
,交 的延长线于
的延长线于 。
。 为黄金矩形。
为黄金矩形。
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
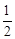 CD,CF=
CD,CF=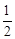 CB则图中阴影部分的面积是 ;(2)若CE=
CB则图中阴影部分的面积是 ;(2)若CE=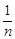 CD,CF=
CD,CF=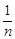 CB,则图中阴影部分的面积是 (用含n的式子表示,n是正整数)
CB,则图中阴影部分的面积是 (用含n的式子表示,n是正整数)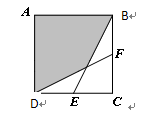
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 = ▲ .
= ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com