
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= ![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 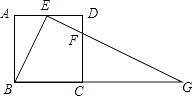
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
【答案】
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴ ![]() ,
,
∵DF= ![]() DC,
DC,
∴ ![]() ,
,
∴ ![]() ,
,
∴△ABE∽△DEF
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴ ![]() ,
,
又∵DF= ![]() DC,正方形的边长为4,
DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10
【解析】(1)利用正方形的性质,可得∠A=∠D,根据已知可得 ![]() ,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;(2)根据平行线分线段成比例定理,可得CG的长,即可求得BG的长.
,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;(2)根据平行线分线段成比例定理,可得CG的长,即可求得BG的长.
【考点精析】关于本题考查的正方形的性质和平行线分线段成比例,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;三条平行线截两条直线,所得的对应线段成比例才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号) 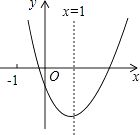
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= ![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 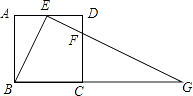
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
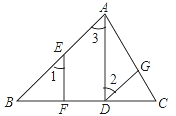
【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中 ![]() 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).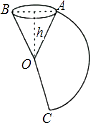
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:
(1)过点________和点_______作直线;
(2)延长线段________到_________,且使________=_________.
(3)过点_________作直线_______的垂线;
(4)作射线_______,使_____平分∠________.
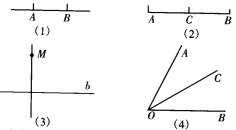
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com