
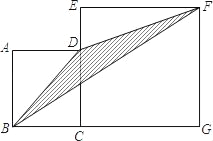
【题目】如图,四边形ABCD和四边形EFBC均为正方形,点D在EC上.如果线段AB的长为5,则△BDF的面积为_____.
【答案】12.5
【解析】
设出正方形EFCG的边长为a,表示出ED与BG,求出三角形EFD的面积,由正方形EFCG的面积-三角形EFD的面积得到四边形DCGF的面积,求出三角形BCD的面积,三角形BDF面积=三角形BCD面积+四边形DCGF的面积-三角形BGF的面积,求出即可.
设正方形EFGC的边长为a,即EC=EF=CG=FG=a,
∴ED=ECDC=a5,BG=BC+CG=a+5,
∴S△EFD=12a(a5),
∴S四边形DCGF=a212a(a5),
∵S△BCD=12×52=12.5,S△BCF=12a(a+5),
∴S△BDF=S△BCD+S四边形DCGFS△BCF=12.5+a212a(a5)12a(a+5)=12.5,
故答案为:12.5.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
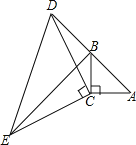
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AB=2cm,则BE=_______cm.
(3)BE与AD有何位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= ![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 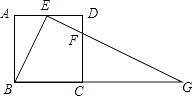
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.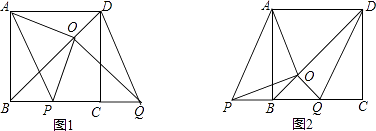
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG. 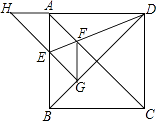
则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
(1)当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(提示:延长MF,交边BC的延长线于点H.)
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;
(3)在(1),(2)的条件下,若BE=![]() ,∠AFM=15°,则AM=.
,∠AFM=15°,则AM=.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.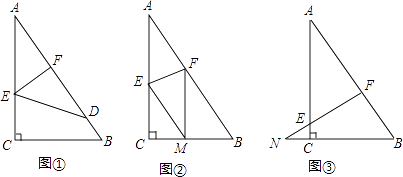
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com