
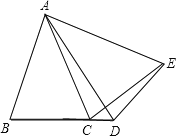
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
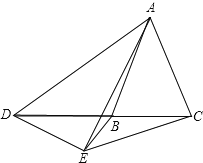
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

【答案】(1)、90°;(2)、①、α+β=180°;理由见解析;②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
【解析】
试题分析:(1)、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出∠BCE=90°;(2)、①、、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出α+β=180°;②、根据题意分别画出两个图形,然后分别进行计算得出答案,当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
试题解析:(1)、90°.
∵∠BAC=∠DAE, ∴∠BAC-∠DAC=∠DAE-∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS),
∴∠B=∠ACE. ∴∠B+∠ACB=∠ACE+∠ACB, ∴∠BCE=∠B+∠ACB, 又∵∠BAC=90° ∴∠BCE=90°
(2)、①α+β=180°,
∵∠BAC=∠DAE, ∴∠BAD+∠DAC=∠EAC+∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS), ∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB. ∴∠B+∠ACB=β, ∵α+∠B+∠ACB=180°, ∴α+β=180°;
②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】京东商城销售A、B两种型号的电风扇,销售单价分别为250元、180元,如表是近两周的销售利润情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)

(1)求A、B两种型号电风扇的每台进价;
(2)若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
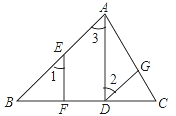
【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中 ![]() 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).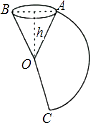
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A( ![]() ,
, ![]() ),点D的坐标为(0,1)
),点D的坐标为(0,1) 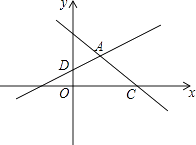
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com