
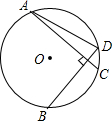
 如图,⊙O的弦AC⊥BD,且$\widehat{AC}$=$\widehat{BD}$,若AD=2$\sqrt{2}$,求⊙O的半径.
如图,⊙O的弦AC⊥BD,且$\widehat{AC}$=$\widehat{BD}$,若AD=2$\sqrt{2}$,求⊙O的半径. 分析 连接OA,OD,BC,CD,先根据圆周角定理得出∠DAE=∠CBE,再由$\widehat{AC}$=$\widehat{BD}$得出$\widehat{AD}$=$\widehat{BC}$,故AC=BD,AD=BC,由AAS定理得出△ADE≌△BCE,故AE=BE,由此可知DE=CE,再由AC⊥BD可知∠DEC=90°,故可得出∠ECD=45°,所以∠AOD=90°,再由勾股定理可得出结论.
解答 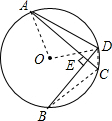 解:连接OA,OD,BC,CD,
解:连接OA,OD,BC,CD,
∵∠DAE与∠CAE是$\widehat{CD}$所对的圆周角,
∴∠DAE=∠CBE.
∵$\widehat{AC}$=$\widehat{BD}$,
∴$\widehat{AD}$=$\widehat{BC}$,
∴AC=BD,AD=BC.
在△ADE与△BCE中,
∵$\left\{\begin{array}{l}∠DAE=∠CBE\\∠AED=∠BEC\\ AD=BC\end{array}\right.$,
∴△ADE≌△BCE(AAS),
∴AE=BE,
∴DE=CE.
∵AC⊥BD,
∴∠DEC=90°,
∴∠ECD=45°,
∴∠AOD=90°.
∴△AOD是等腰直角三角形.
∵AD=2$\sqrt{2}$,2AO2=AD2,即2AO2=(2$\sqrt{2}$)2,解得AO=2.
答:⊙O的半径等于2.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 726 | B. | 594 | C. | 328 | D. | 324 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
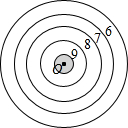 如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm.
如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )| A. |  | B. | 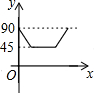 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com