【题目】公园的门票价格规定如下表：
购票张数 | 1 到 50 张 | 51 到 100 张 | 101 到 150张 | 150 张以上 |
每张票的价格 | 12 元 | 10 元 | 8 元 | 超过 150 张的部分 7 元 |
某校七年级（1）（2）两个班共 104 人，其中（1）班 40 多人，不足 50 人，经估算，如果两个班都以班为单位购票，则一共应付 1136 元，问：
(1)若两班联合起来作为一个团体购票，可省多少钱？
(2)两班学生各有多少人？
(3)若七年级（3）班有 n 人（46<n<55）与（1）,（2）班一起去游园，某商家赞助，支付三个班的所有门票费，则该商家最少花费 元（用含 n 的式子表示）
【答案】（1）304元；（2）七年级（1）班有48人，七年级（2）班有56人；（3）(7n+1178).
【解析】
（1）先求出购团体票的费用，再用1136元－团体票的费用就是节约的钱；
（2）设七年级（1）班有x人，则七年级（2）班有（104－x）人，根据两个班共付费1136元建立方程求出其解就可以；
（3）表示出总人数，判断范围，分段列式计算即可.
（1）由题意，得
1136104×8=304元.
答：两班联合起来，作为一个团体购票，可省304元；
（2）设七年级（1）班有x人，则七年级（2）班有(104x)人，由题意，得
12x+10(104x)=1136，
解得：x=48，
∴七年级（2）班有学生：10448=56人.
答：七年级（1）班有48人，则七年级（2）班有56人；
（3）由题知，三个班总人数为（104+n）人，
∵46<n<55，
∴104+n>150，
∴费用为：
元
寒假乐园北京教育出版社系列答案科目：初中数学 来源： 题型：
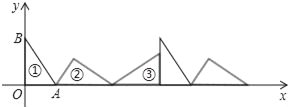
【题目】如图①为Rt△AOB，∠AOB=90°，其中OA=3，OB=4．将AOB沿x轴依次以A，B，O为旋转中心顺时针旋转．分别得图②，图③，…，则旋转到图⑩时直角顶点的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究与发现：
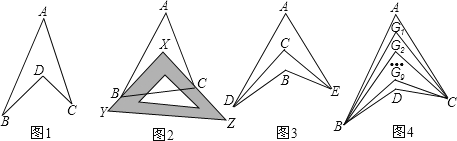
如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：
（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
（2）请你直接利用以上结论，解决以下三个问题：
①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝50°，则∠ABX+∠ACX＝ °；
②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝50°，∠DBE＝130°，求∠DCE的度数；
③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC＝140°，∠BG1C＝77°，求∠A的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，线段AD=10cm，点B，C都是线段AD上的点，且AC=7cm，BD=4cm，若E，F分别是线段AB，CD的中点，求BC与EF的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有理数 a，b，c 分别对应数轴上的点 A,B,C,若a 2
|b 4| 0 ，关于 x、y 的单项式3(c 3)x
y与 yx 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记，例如，点 A 与点 B 间的距离记作 AB.
(1)求 a，b，c 的值；
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动：第一回合，从点 C 到点 B 到点 A 回到点 C；第二回合，从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C；第三回合，从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……，如此循环下去，若第 t 秒时满足 PB+2PC=AC+1，求 t 的最大值；
(3)在（2）的条件下，P 点第一次从 C 点出发的同时，数轴上的动点 M、N 分别从 A 点和 B 点向右运动，速度分别为每秒 1 个单位长度和每秒 2 个单位长度，P 点完成第一个回合后停止在 C 点，当 MP=2MN 时， t 的值是 （直接填答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题：
（1）将下面的表格补充完整：
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
（2）根据规律，是否存在一个正多边形，其中的∠α＝21°？若存在，请求出n的值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
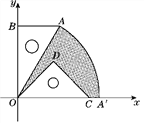
【题目】如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把这两块三角板放置在平面直角坐标系中，且OB＝3
.
(1)若某反比例函数的图象的一个分支恰好经过点A，求这个反比例函数的解析式；
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好落在x轴上，点A落在点A′处，试求图中阴影部分的面积．(结果保留π)
【答案】(1)反比例函数的解析式为y＝
；(2)S阴影＝6π－
.
【解析】分析：（1）根据tan30°=
，求出AB，进而求出OA，得出A的坐标，设过A的双曲线的解析式是y=
，把A的坐标代入求出即可；（2）求出∠AOA′，根据扇形的面积公式求出扇形AOA′的面积，求出OD、DC长，求出△ODC的面积，相减即可求出答案．
本题解析：
(1)在Rt△OBA中，∠AOB＝30°，OB＝3
，
∴AB＝OB·tan 30°＝3.
∴点A的坐标为(3，3)．
设反比例函数的解析式为y＝
(k≠0)，
∴3＝
，∴k＝9，则这个反比例函数的解析式为y＝
.
(2)在Rt△OBA中，∠AOB＝30°，AB＝3，
sin ∠AOB＝
，即sin 30°＝
，
∴OA＝6.
由题意得：∠AOC＝60°，S扇形AOA′＝
＝6π.
在Rt△OCD中，∠DOC＝45°，OC＝OB＝3，
∴OD＝OC·cos 45°＝3×
＝
.
∴S△ODC＝
OD2＝
＝
.
∴S阴影＝S扇形AOA′－S△ODC＝6π－.
点睛：本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质，本题属于中档题，难度不大，将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
26
【题目】矩形ABCD一条边AD＝8，将矩形ABCD折叠，使得点B落在CD边上的点P处．
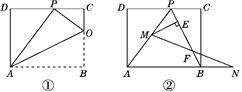
(1)如图①，已知折痕与边BC交于点O，连接AP，OP，OA.
① 求证：△OCP∽△PDA；
② 若△OCP与△PDA的面积比为1:4，求边AB的长．
(2)如图②，在(1)的条件下，擦去AO和OP，连接BP.动点M在线段AP上(不与点P，A重合)，动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E.试问动点M，N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整．
收集数据：
从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：
千家店镇：120 115 100 100 95 85 80 70 50 50 50 45
永宁 镇：110 90 105 80 90 85 90 60 90 45 70 60
整理、描述数据：
空气质量
按如表整理、描述这两镇空气污染指数的数据：
空气质量为优 | 空气质量为良 | 空气质量为轻微污染 | |
千家店镇 | 4 | 6 | 2 |
永宁 镇 |
|
|
|
（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）
分析数据：
两镇的空气污染指数的平均数、中位数、众数如下表所示；
城镇 | 平均数 | 中位数 | 众数 |
千家店 | 80 |
| 50 |
永 宁 | 81.3 | 87.5 |
|
请将以上两个表格补充完整；
得出结论：可以推断出 镇这一年中环境状况比较好，理由为 ．（至少从两个不同的角度说明推断的合理性）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
