
����Ŀ����ͼ�������� a��b��c �ֱ��Ӧ�����ϵĵ� A,B,C,��a 2![]() |b 4| 0 ������ x��y �ĵ���ʽ3(c 3)x
|b 4| 0 ������ x��y �ĵ���ʽ3(c 3)x![]() y
y![]() �� y
�� y![]() x ��ͬ����. ���ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ���ǣ����磬�� A ��� B ��ľ������ AB.
x ��ͬ����. ���ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ���ǣ����磬�� A ��� B ��ľ������ AB.
![]()
![]()
(1)�� a��b��c ��ֵ��
(2)�� P �� C �������ÿ�� 1 ����λ�����������ϰ����¹��������˶�����һ�غϣ��ӵ� C ���� B ���� A �ص��� C���ڶ��غϣ��ӵ� C �� BC ���е� D �� CA ���е� D1 �ص��� C�������غϣ��ӵ� C �� CD ���е� D2 �� CD1 ���е� D3 �ص��� C���������ѭ����ȥ������ t ��ʱ���� PB+2PC=AC+1���� t �����ֵ��
(3)�ڣ�2���������£�P ���һ�δ� C �������ͬʱ�������ϵĶ��� M��N �ֱ�� A ��� B �������˶����ٶȷֱ�Ϊÿ�� 1 ����λ���Ⱥ�ÿ�� 2 ����λ���ȣ�P ����ɵ�һ���غϺ�ֹͣ�� C �㣬�� MP=2MN ʱ�� t ��ֵ�� ��ֱ����𰸣�
���𰸡���1��a=2��b=��4��c=��1����2�����ֵΪ![]() �룻��3��
�룻��3��![]() ��.
��.
��������
��1�����ݾ���ֵ��ż���ݵķǸ��Կ������a��b���ٸ���ͬ����Ķ�����c����.
��2�����ȸ��ݵ�һ�غϼ��������PB+2PC=AC+1ʱ��tֵ���Ӷ��õ�Ҫ����PB+2PC=AC+1�ĵ�P����Ӧ���������������ڼ��غϵ��ﲻ����������Ӷ������ֵ��
��3������N��Mʱt��ֵ���ݴ˽��з�������.
��1����![]() ��3(c 3)x
��3(c 3)x![]() y
y![]() �� y
�� y![]() x ��ͬ����
x ��ͬ����
��a��2=0��b+4=0��|c+2|=1��c+3��0��
��a=2��b=��4��c=��1.
��2���ɣ�1��֪����A��Ӧ����Ϊ2����B��Ӧ����Ϊ��4����C��Ӧ����Ϊ��1����AC=3��
��һ�غϣ�����P��C��Bʱ��CP=t��BP=3��t��
��PB+2PC=AC+1
��3��t+2t=4����t=1����ʱ��P��Ӧ����Ϊ��2��
����P��C��Aʱ��CP=t��6��BP=3+t��6=t��3��
��PB+2PC=AC+1
��t��3+2(t��6)=4����t=![]() ����ʱ��P��Ӧ����Ϊ
����ʱ��P��Ӧ����Ϊ![]() ��
��
ͨ������ɵã�D4��Ӧ����Ϊ![]() ��D5��Ӧ����Ϊ
��D5��Ӧ����Ϊ![]() ��D6��Ӧ����Ϊ
��D6��Ӧ����Ϊ![]() >��2��D7��Ӧ����Ϊ
>��2��D7��Ӧ����Ϊ![]() <
<![]() ������t�����ֵ�ڵ����غϵ�P��D5�ص���Cʱȡ��.
������t�����ֵ�ڵ����غϵ�P��D5�ص���Cʱȡ��.
��ʱCP= ![]() ��BP=
��BP= ![]() ��
��
��![]() ����
����![]() ��
��
������PB+2PC=AC+1ʱ��t�����ֵΪ![]() ��.
��.
��3������ɵã�AC==BC=3����P�˶�·��Ϊt����M�˶�·��Ϊt����N�˶�·��Ϊ2t��
��2t��t=6�����t=6�����˶�6���N��M��
����ǰ��![]() ����MN=6+t��2t=6��t��
����MN=6+t��2t=6��t��
��![]() ʱ��MP=t+3+t=2t+3����2t+3=2(6��t)�����
ʱ��MP=t+3+t=2t+3����2t+3=2(6��t)�����![]() ��
��
��![]() ʱ��MP= t+3+(6��t)=9����9=2(6��t)�����
ʱ��MP= t+3+(6��t)=9����9=2(6��t)�����![]() ��������������ȥ��
��������������ȥ��
���Ϻ�![]() ����MN=2t��6��t =t��6��
����MN=2t��6��t =t��6��
��![]() ʱ��MP=9��t+t=9����9=2(t��6)�����
ʱ��MP=9��t+t=9����9=2(t��6)�����![]() ��������������ȥ��
��������������ȥ��
��![]() ʱ��MP= t��9+t=2t��9����2t��9=2(t��6)���⣻
ʱ��MP= t��9+t=2t��9����2t��9=2(t��6)���⣻
����������tֵΪ![]() ��.
��.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
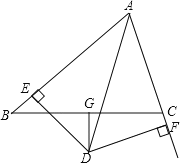
����Ŀ����ͼ����ABC�У�ADƽ�֡�BAC��DG��BC��ƽ��BC��DE��AB��E��DF��AC��F��
��1���ж�BE��CF��������ϵ����˵�����ɣ�
��2�����AB=8��AC=6����AE��BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����涨����һ�����㣺a��b=![]() (|ab|+a+b)�����磺2��3=
(|ab|+a+b)�����磺2��3=![]() (|23|+2+3)=3
(|23|+2+3)=3
��1����3��4�ͣ�-3������-2����ֵ��
��2����1,2,3,��,50��50����Ȼ��,�����Ϊ25��,ÿ��������,�ֽ�ÿ�������������һ��ֵ����a,��һ������b,�������ʽ![]() (|ab|+a+b)�н��м��㣬���������25�������������25��ֵ������25��ֵ�ĺ͵����ֵ��_____.
(|ab|+a+b)�н��м��㣬���������25�������������25��ֵ������25��ֵ�ĺ͵����ֵ��_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
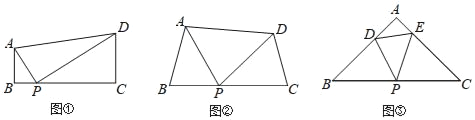
����Ŀ����ͼ�٣����ı���ABCD�У�AB��CD����B=90������P��BC���ϣ�����APD=90�� ʱ����֪��ABP�ס�PCD������Ҫ��֤����
��1��̽������ͼ�ڣ����ı���ABCD�У���P��BC���ϣ�����B=��C=��APDʱ����֤����ABP�ס�PCD��
��2����չ����ͼ�ۣ�����ABC�У���P�DZ�BC���е㣬��D��E�ֱ��ڱ�AB��AC������B=��C=��DPE=45����BC=8![]() ��CE=6����DE�ij�Ϊ�� ����
��CE=6����DE�ij��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ʊ�۸�涨���±���
��Ʊ���� | 1 �� 50 �� | 51 �� 100 �� | 101 �� 150�� | 150 ������ |
ÿ��Ʊ�ļ۸� | 12 Ԫ | 10 Ԫ | 8 Ԫ | ���� 150 �ŵIJ��� 7 Ԫ |
ijУ���꼶��1����2������� 104 �ˣ����У�1���� 40 ���ˣ����� 50 �ˣ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ�� 1136 Ԫ���ʣ�
(1)����������������Ϊһ�����幺Ʊ����ʡ����Ǯ��
(2)����ѧ�����ж����ˣ�
(3)�����꼶��3������ n �ˣ�46<n<55���루1��,��2����һ��ȥ����ij�̼�������֧���������������Ʊ�ѣ�����̼����ٻ��� Ԫ���ú� n ��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BE��CF�ֱ���AC��AB�����ϵĸߣ���BE�Ͻ�ȡBD=AC����CF���ӳ����Ͻ�ȡCG=AB������AD��AG��
��1����֤��AD=AG��
��2��AD��AG��λ�ù�ϵ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ı�AB��x���ϣ���C������Ϊ����5��4������D��y����������ϣ�������A��ֱ��y��![]() x��1��y�ύ�ڵ�E����ֱ��AE��y������ƽ��n��n��0������λ���Ⱥõ�ֱ��l��ֱ��l������Cʱֹͣƽ�ƣ�
x��1��y�ύ�ڵ�E����ֱ��AE��y������ƽ��n��n��0������λ���Ⱥõ�ֱ��l��ֱ��l������Cʱֹͣƽ�ƣ�
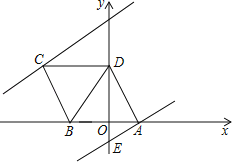
��1����A�������� ������B�������� ����
��2����ֱ��l��y���ڵ�F������CF�����CDF�����ΪS������涨���߶������Ϊ0�������Σ�����S��n֮��ĺ�����ϵʽ����д��n��ȡֵ��Χ��
��3����֪AE��AD�ڵ�A,��ֱ��l������AD��DC�ڵ�P������AEPΪֱ��������ʱ����ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��2����֪�ı���ABCDΪ�����Σ�������AC����һ����P����PE��AD�����ӳ��ߣ���E����PF��DC�����ӳ��ߣ���F��������BP��EF��G��
��1����ͼ1�У���������ABCD�ı߳�Ϊ2���ı���ABFE�����Ϊy��AP=x����y����x�ĺ�������ʽ��
��2�����ۣ�GB��EF��ͼ1��ͼ2���dz����ģ�����ѡһͼ�θ���֤����
��3�������ͼ2֤������FGC�ס�PFB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѱ߳�Ϊ2�ĵȱ���������ABC��ֱ��BC����ƽ�ƣ�ʹ��B���C�غϣ��õ���DCE������BD����AC�ڵ�F��
��1��֤����AC��BD��
��2�����߶�BD�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com