
【题目】如图,把边长为2的等边三角形△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.
(1)证明:AC⊥BD;
(2)求线段BD的长。

【答案】(1)证明见解析(2)2![]()
【解析】
(1)由平移的性质可知BE=2BC=6,DE=AC=3,故可得出BD⊥DE,由∠E=∠ACB=60°可知AC∥DE,故可得出结论;
(2)在Rt△BDE中利用勾股定理即可得出BD的长.
(1)∵△DCE由△ABC平移而成,
∴BE=2BC=4,DE=AC=2,∠E=∠ACB=60°,
∴DE=![]() BE,
BE,
∴BD⊥DE,
又∵∠E=∠ACB=60°,
∴AC∥DE,
∴BD⊥AC,
∵△ABC是等边三角形,
∴BF是边AC的中线,
∴BD⊥AC,BD与AC互相垂直平分;
(2)∵由(1)知,AC∥DE,BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴BD=![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,有理数 a,b,c 分别对应数轴上的点 A,B,C,若a 2![]() |b 4| 0 ,关于 x、y 的单项式3(c 3)x
|b 4| 0 ,关于 x、y 的单项式3(c 3)x![]() y
y![]() 与 y
与 y![]() x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
![]()
![]()
(1)求 a,b,c 的值;
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动:第一回合,从点 C 到点 B 到点 A 回到点 C;第二回合,从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C;第三回合,从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……,如此循环下去,若第 t 秒时满足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的条件下,P 点第一次从 C 点出发的同时,数轴上的动点 M、N 分别从 A 点和 B 点向右运动,速度分别为每秒 1 个单位长度和每秒 2 个单位长度,P 点完成第一个回合后停止在 C 点,当 MP=2MN 时, t 的值是 (直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
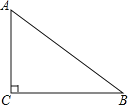
【题目】已知:在Rt△ABC中,∠C=90°.
(1)请在线段BC上作一点D,使点D到边AC、AB的距离相等(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=6,BC=8,请求出CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从北京市环保局证实,为满足2022年冬奥会对环境质量的要求,北京延庆正在对其周边的环境污染进行综合治理,率先在部分村镇进行“煤改电”改造.在治理的过程中,环保部门随机选取了永宁镇和千家店镇进行空气质量监测.过程如下,请补充完整.
收集数据:
从2016年12月初开始,连续一年对两镇的空气质量进行监测(将30天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,12个月的空气污染指数如下:
千家店镇:120 115 100 100 95 85 80 70 50 50 50 45
永宁 镇:110 90 105 80 90 85 90 60 90 45 70 60
整理、描述数据:
空气质量
按如表整理、描述这两镇空气污染指数的数据:
空气质量为优 | 空气质量为良 | 空气质量为轻微污染 | |
千家店镇 | 4 | 6 | 2 |
永宁 镇 |
|
|
|
(说明:空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.)
分析数据:
两镇的空气污染指数的平均数、中位数、众数如下表所示;
城镇 | 平均数 | 中位数 | 众数 |
千家店 | 80 |
| 50 |
永 宁 | 81.3 | 87.5 |
|
请将以上两个表格补充完整;
得出结论:可以推断出 镇这一年中环境状况比较好,理由为 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC
.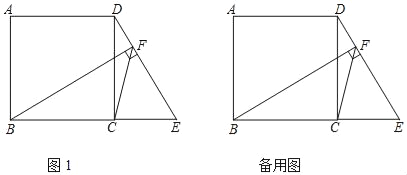
(1)求证:∠FBC=∠CDF.
(2)作点C关于直线DE的对称点G,连接CG,FG.
①依据题意补全图形;
②用等式表示线段DF,BF,CG之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
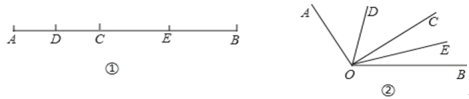
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣kx+k2+n=0有两个不相等的实数根x1、x2,且(2x1+x2)2﹣8(2x1+x2)+15=0.
(1)求证:n<0;
(2)试用k的代数式表示x1;
(3)当n=﹣3时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com