
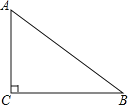
【题目】已知:在Rt△ABC中,∠C=90°.
(1)请在线段BC上作一点D,使点D到边AC、AB的距离相等(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=6,BC=8,请求出CD的长度.
【答案】(1)见解析(2)3.
【解析】
(1)根据角平分线上的点到角的两边距离相等知作出∠A的平分线即可;
(2)设CD的长为x,然后用x表示出DB、DE、BF利用勾股定理得到有关x的方程,解之即可.
(1)如图所示:所以点D为所求;
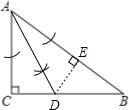
(2)过点D做DE⊥AB于E,设DC=x,则BD=8-x
∵Rt△ABC中,∠C=90°,AC=6,BC=8
∴由勾股定理得AB=![]()
∵点D到边AC、AB的距离相等
∴AD是∠BAC的平分线
又∵∠C=90°,DE⊥AB
∴DE=DC=x,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=4,
Rt△DEB中,∠DEB=90°,
∴由勾股定理得DE2+BE2=BD2,
即x2+42=(8-x)2,
解得x=3.
答:CD的长度为3.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
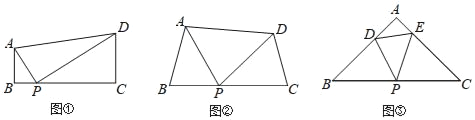
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90° 时,可知△ABP∽△PCD.(不要求证明)
(1)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
(2)拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上若∠B=∠C=∠DPE=45°,BC=8![]() ,CE=6,则DE的长为 .
,CE=6,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一方队正沿箭头所指的方向前进

(1)A的位置为第三列第四行,表示为(3,4),那么B的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)B左侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)如果队伍向东前进,那么A北侧第二个人的位置是____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4)![]() 表示的位置是____________.
表示的位置是____________.
A.A B.B C.C D.D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上有A、B、C三点,且AB=3BC,若B为原点,A点表示数为6.
(1)求C点表示的数;
(2)若数轴上有一动点P,以每秒1个单位的速度从点C向点A匀速运动,设运动时间为t秒,请用含t的代数式表示PB的长;
(3)在(2)的条件下,点P运动的同时有一动点Q从点A以每秒2个单位的速度向点C匀速运动,当P、Q两点相距2个单位长度时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )

A. 2![]() B. 3
B. 3![]() C. 6
C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为2的等边三角形△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.
(1)证明:AC⊥BD;
(2)求线段BD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com