
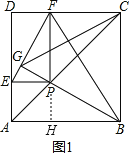
【题目】如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.

【答案】(1)y=x2+2;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)根据题意得出S四边形ABFE=4﹣ED×DF﹣BC×FC进而得出答案;
(2)首先利用正方形的性质进而证明△FPE≌△BHP(SAS),即可得出△FPG∽△BPH,求出即可;
(3)首先得出△DPC≌△BPC(SAS),进而利用相似三角形的判定得出△FGC∽△PFB.
试题解析:(1)解:∵PE⊥AD,PF⊥DC,
∴四边形EPFD是矩形,
∵AP=x,
∴AE=EP=DF=![]() x,
x,
DE=PF=FC=2﹣![]() x,
x,
∴S四边形ABFE=4﹣EDDF﹣BCFC=x2+2;
(2)证明:如图1,延长FP交AB于H,
∵PF⊥DC,PE⊥AD,
∴PF⊥PE,PH⊥HB,
即∠BHP=90°,
∵四边形ABCD是正方形,
∴AC平分∠DAB,
∴可得PF=FC=HB,EP=PH,
在△FPE与△BHP中
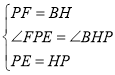 ,
,
∴△FPE≌△BHP(SAS),
∴∠PFE=∠PBH,
又∵∠FPG=∠BPH,
∴△FPG∽△BPH,
∴∠FGP=∠BHP=90°,
即GB⊥EF;
(3)证明:如图2,连接PD,

∵GB⊥EF,
∴∠BPF=∠CFG①,
在△DPC和△BPC中
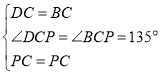 ,
,
∴△DPC≌△BPC(SAS),
∴PD=PB,
而PD=EF,∴EF=PB,
又∵GB⊥EF,
∴PF2=FGEF,
∴PF2=FGPB,
而PF=FC,
∴PFFC=FGPB,
∴![]() ②,
②,
∴由①②得△FGC∽△PFB.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
(1)点P在运动过程中,若某一时刻,△OPA的面积为6,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?(只需写出t的值,无需解答过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有理数 a,b,c 分别对应数轴上的点 A,B,C,若a 2![]() |b 4| 0 ,关于 x、y 的单项式3(c 3)x
|b 4| 0 ,关于 x、y 的单项式3(c 3)x![]() y
y![]() 与 y
与 y![]() x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
![]()
![]()
(1)求 a,b,c 的值;
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动:第一回合,从点 C 到点 B 到点 A 回到点 C;第二回合,从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C;第三回合,从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……,如此循环下去,若第 t 秒时满足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的条件下,P 点第一次从 C 点出发的同时,数轴上的动点 M、N 分别从 A 点和 B 点向右运动,速度分别为每秒 1 个单位长度和每秒 2 个单位长度,P 点完成第一个回合后停止在 C 点,当 MP=2MN 时, t 的值是 (直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A对应的数是-6,点B对应的数是-2,点O对应的数是0.动点P、Q分别从A、B同时出发,以每秒3个单位,每秒1个单位的速度向右运动。在运动过程中,线段PQ的长度始终是另一线段长的整数倍,这条线段是( )

A.PBB.OPC.OQD.QB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3![]() .
.
(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
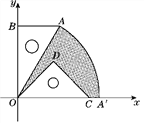
【答案】(1)反比例函数的解析式为y=![]() ;(2)S阴影=6π-
;(2)S阴影=6π-![]() .
.
【解析】分析:(1)根据tan30°=![]() ,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=
,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=![]() ,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
本题解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴点A的坐标为(3,3![]() ).
).
设反比例函数的解析式为y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,则这个反比例函数的解析式为y=
,则这个反比例函数的解析式为y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由题意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S阴影=S扇形AOA′-S△ODC=6π-![]() .
.
点睛:本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质,本题属于中档题,难度不大,将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
26
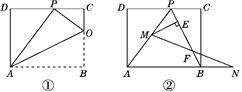
【题目】矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O,连接AP,OP,OA.
① 求证:△OCP∽△PDA;
② 若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
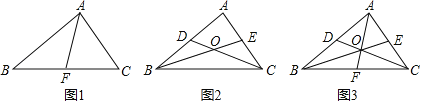
【题目】问题解决:如图1,△ABC中,AF为BC边上的中线,则S△ABF= S△ABC.
问题探究:
(1)如图2,CD,BE分别是△ABC的中线,S△BOC与S四边形ADOE相等吗?
解:△ABC中,由问题解决的结论可得,S△BCD=![]() S△ABC,S△ABE=
S△ABC,S△ABE=![]() S△ABC.
S△ABC.
∴S△BCD=S△ABE
∴S△BCD﹣S△BOD=S△ABE﹣S△BOD
即S△BOC=S四边形ADOE.
(2)图2中,仿照(1)的方法,试说明S△BOD=S△COE.
(3)如图3,CD,BE,AF分别是△ABC的中线,则S△BOC= S△ABC,S△AOE= S△ABC,S△BOD= S△ABF.
问题拓展:
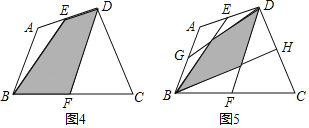
(4)①如图4,E、F分别为四边形ABCD的边AD、BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
②如图5,E、F、G、H分别为四边形ABCD的边AD、BC、AB、CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
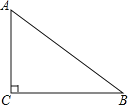
【题目】已知:在Rt△ABC中,∠C=90°.
(1)请在线段BC上作一点D,使点D到边AC、AB的距离相等(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=6,BC=8,请求出CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com