
【题目】如图,一次函数![]() 的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
(1)点P在运动过程中,若某一时刻,△OPA的面积为6,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?(只需写出t的值,无需解答过程)

【答案】(1)(2,4.5),(-2,7.5);(2)2.8,4,5,16
【解析】试题分析:(1)先求出△OPA的面积为6时BP的长,再求出点P的坐标;(2)分别讨论AO=AP,AP=OP和AO=OP三种情况.
解:(1)在y=-![]() x+6中,令x=0,得y=6,令y=0,得x=8,
x+6中,令x=0,得y=6,令y=0,得x=8,
∴A(0,6),B(8,0),
∴OA=6,OB=8,∴AB=10,
∴AB边上的高为6×8÷10=![]() ,
,
∵P点的运动时间为t,∴BP=t,则AP=![]() ,
,
当△AOP面积为6时,则有![]() AP×
AP×![]() =6,即
=6,即![]() ×
×![]() =6,解得t=7.5或12.5,
=6,解得t=7.5或12.5,
过P作PE⊥x轴,PF⊥y轴,垂足分别为E、F,
则PE=![]() =4.5或7.5,BE=
=4.5或7.5,BE=![]() =6或10,
=6或10,
则点P坐标为(8-6,4.5)或(8-10,7.5),即(2,4.5)或(-2,7.5);
(2)由题意可知BP=t,AP=![]() ,
,
当△AOP为等腰三角形时,有AP=AO、AP=OP和AO=OP三种情况.
①当AP=AO时,则有![]() =6,解得t=4或16;
=6,解得t=4或16;
②当AP=OP时,过P作PM⊥AO,垂足为M,如图1,
则M为AO中点,故P为AB中点,此时t=5;
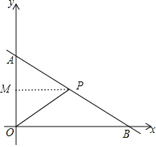

图1 图2
③当AO=OP时,过O作ON⊥AB,垂足为N,过P作PH⊥OB,垂足为H,如图2,
则AN=![]() AP=
AP=![]() (10-t),
(10-t),
∵PH∥AO,∴△AOB∽△PHB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴PH=
,∴PH=![]() t,
t,
又∠OAN+∠AON=∠OAN+PBH=90°,
∴∠AON=∠PBH,又∠ANO=∠PHB,
∴△ANO∽△PHB,![]() =
=![]() ,即
,即![]() =
=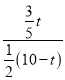 ,解得t=
,解得t=![]() ;
;
综上可知当t的值为![]() 、4、5和16时,△AOP为等腰三角形.
、4、5和16时,△AOP为等腰三角形.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求代数式的值: ![]() ,其中m=1.
,其中m=1.
【答案】(1) ![]() ,
, ![]()
【解析】先进行分式的混合运算,再代入求值即可.
解:原式= ,
,
= ,
,
=![]() ;
;
当m =1时,原式=![]() =-
=-![]() .
.
【题型】解答题
【结束】
25
【题目】如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
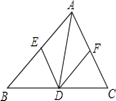
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).
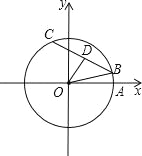
A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x﹣6与反比例函数![]() 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com