【题目】先化简，再求代数式的值： 
，其中m＝1．
【答案】(1) 
， 
【解析】先进行分式的混合运算，再代入求值即可.
解：原式＝
，
＝
，
＝
；
当m ＝1时，原式＝
＝－
．
【题型】解答题
【结束】
25
【题目】如图，在△ABC中，D为BC边的中点，过D点分别作DE∥AB交AC于点E，DF∥AC交AB于点F．
求证：BF=DE．
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案科目：初中数学 来源： 题型：
【题目】如图所示，在8×8的网络中，△ABC是格点三角形(顶点是网格线的交点），若点A坐标为（-1,3），按要求回答下列问题：
（1）建立符合条件的平面直角坐标系，并写出点B和点C的坐标；
（2）将△ABC先向下平移2个单位长度，在向右平移3个单位长度，得到△DEF，请在图中画出△DEF，并求出线段AC在平移过程中扫过的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点A、B、C在数轴上对应的数分别为1、3、5，点P在数轴上对应的数是﹣2，点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，…，则P1P2016的长度为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列从左边到右边的变形，因式分解正确的是（ ）
A. 2a2﹣2=2(a+1)(a﹣1) B. (a+3)(a﹣3)=a2﹣9
C. ﹣ab2+2ab﹣3b=﹣b(ab﹣2a﹣3) D. x2﹣2x﹣3=x(x﹣2)﹣3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：∠C=∠D，OD=OC．求证：DE=CE．
【答案】证明见解析
【解析】试题分析：利用ASA证明△OBC≌△OAD，根据全等三角形的对应边相等可得OA=OB，再由OD=OC，即可得AC=BD，根据AAS证明△ACE≌△BDE，再由全等三角形的对应边相等即可得结论.
试题解析：
在△OBC和△OAD中，
，
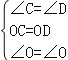∴△OBC≌△OAD（ASA），
∴OA=OB，
∵OD=OC，
∴OD﹣OB=OC﹣OA，即AC=BD，
在△ACE和△BDE中，
，
∴△ACE≌△BDE（AAS），
∴DE=CE．
【题型】解答题
【结束】
27
【题目】如图，以等腰直角三角形ABC的斜边AB为边向内作等边△ABD，连接DC，以DC为边，作等边△DCE，点B、E在CD的同侧．
（1）求∠BCE的大小；
（2）求证：BE=AC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于O点，且BE=BF，∠BEF=2∠BAC。
（1）求证：OE=OF；
（2）若BC=
，求AB的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图像分别交y轴、x轴交于点A、B，点P从点B出发，沿射线BA以每秒1个单位的速度出发，设点P的运动时间为t秒.
（1）点P在运动过程中，若某一时刻，△OPA的面积为6,求此时P的坐标；
（2）在整个运动过程中，当t为何值时，△AOP为等腰三角形？（只需写出t的值，无需解答过程）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
