
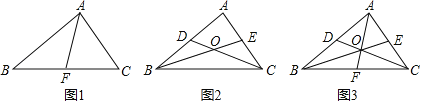
ЎҫМвДҝЎҝОКМвҪвҫцЈәИзНј1Ј¬ЎчABCЦРЈ¬AFОӘBCұЯЙПөДЦРПЯЈ¬ФтSЎчABFЈҪЎЎ ЎЎSЎчABCЈ®
ОКМвМҪҫҝЈә
ЈЁ1Ј©ИзНј2Ј¬CDЈ¬BE·ЦұрКЗЎчABCөДЦРПЯЈ¬SЎчBOCУлSЛДұЯРОADOEПаөИВрЈҝ
ҪвЈәЎчABCЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬SЎчBCDЈҪ![]() SЎчABCЈ¬SЎчABEЈҪ
SЎчABCЈ¬SЎчABEЈҪ![]() SЎчABCЈ®
SЎчABCЈ®
ЎаSЎчBCDЈҪSЎчABE
ЎаSЎчBCD©ҒSЎчBODЈҪSЎчABE©ҒSЎчBOD
јҙSЎчBOCЈҪSЛДұЯРОADOEЈ®
ЈЁ2Ј©Нј2ЦРЈ¬·ВХХЈЁ1Ј©өД·Ҫ·ЁЈ¬КФЛөГчSЎчBODЈҪSЎчCOEЈ®
ЈЁ3Ј©ИзНј3Ј¬CDЈ¬BEЈ¬AF·ЦұрКЗЎчABCөДЦРПЯЈ¬ФтSЎчBOCЈҪЎЎ ЎЎSЎчABCЈ¬SЎчAOEЈҪЎЎ ЎЎSЎчABCЈ¬SЎчBODЈҪЎЎ ЎЎSЎчABFЈ®
ОКМвНШХ№Јә
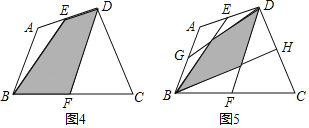
ЈЁ4Ј©ўЩИзНј4Ј¬EЎўF·ЦұрОӘЛДұЯРОABCDөДұЯADЎўBCөДЦРөгЈ¬ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРОABCDөДГж»эЦ®јдөДКэБҝ№ШПөЈәSТхУ°ЈҪЎЎ ЎЎSЛДұЯРОABCDЈ®
ўЪИзНј5Ј¬EЎўFЎўGЎўH·ЦұрОӘЛДұЯРОABCDөДұЯADЎўBCЎўABЎўCDөДЦРөгЈ¬ЗлЦұҪУРҙіцТхУ°Іҝ·ЦөДГж»эУлЛДұЯРОABCDөДГж»эЦ®јдөДКэБҝ№ШПөЈәSТхУ°ЈҪЎЎ ЎЎSЛДұЯРОABCDЈ®
Ўҫҙр°ёЎҝОКМвҪвҫцЈә![]() Ј»ОКМвМҪҫҝЈәЈЁ2Ј©ЦӨГчјыҪвОцЈ»ЈЁ3Ј©
Ј»ОКМвМҪҫҝЈәЈЁ2Ј©ЦӨГчјыҪвОцЈ»ЈЁ3Ј©![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»ОКМвНШХ№ЈәЈЁ4Ј©ўЩ
Ј»ОКМвНШХ№ЈәЈЁ4Ј©ўЩ![]() Ј»ўЪ
Ј»ўЪ![]() .
.
ЎҫҪвОцЎҝ
ОКМвҪвҫцЈәёщҫЭЦРПЯөДРФЦКјҙҝЙөГіцҪбВЫЈ»
ОКМвМҪҫҝЈәЈЁ2Ј©ёщҫЭОКМвҪвҫцөДҪбВЫҝЙөГЈ¬SЎчBCDЈҪ![]() SЎчABCЈ¬SЎчBCEЈҪ
SЎчABCЈ¬SЎчBCEЈҪ![]() SЎчABCЈ¬И»әуёщҫЭөИКҪөД»щұҫРФЦКјҙҝЙөГіцSЎчBODЈҪSЎчCOEЈ»
SЎчABCЈ¬И»әуёщҫЭөИКҪөД»щұҫРФЦКјҙҝЙөГіцSЎчBODЈҪSЎчCOEЈ»
ЈЁ3Ј©ёщҫЭЦРПЯөДРФЦКәНМҪҫҝҪбВЫЈЁ1Ј©ЈЁ2Ј©ҝЙНЖіцSЎчAOEЈҪSЎчAODЈҪSЎчBOFЈҪSЎчCOFЈҪSЎчBODЈҪSЎчCOEЈҪ![]() SЎчABCЈ¬ҙУ¶шөГіцҪбВЫЈ»
SЎчABCЈ¬ҙУ¶шөГіцҪбВЫЈ»
ОКМвНШХ№ЈәЈЁ4Ј©ўЩБ¬ҪУBDЈ¬ёщҫЭЦРПЯөДРФЦКҝЙөГSЎчABEЈҪSЎчBDEәНSЎчBDFЈҪSЎчDFCЈ¬ҙУ¶шөГіцҪбВЫЈ»ўЪБ¬ҪУBDЈ¬ЙиBEҪ»DGУЪMЈ¬BHҪ»DFУЪNЈ¬ёщҫЭОКМвМҪҫҝЈәЈЁ3Ј©өДҪбВЫЈ¬ҝЙөГSЎчBDMЈҪ![]() SЎчABDЈ¬SЎчBDNЈҪ
SЎчABDЈ¬SЎчBDNЈҪ![]() SЎчBDCЈ¬Ј¬ҙУ¶шөГіцҪбВЫЈ®
SЎчBDCЈ¬Ј¬ҙУ¶шөГіцҪбВЫЈ®
ҪвЈәОКМвҪвҫцЈәЎЯAFКЗBCұЯЙПөДЦРПЯЈ¬
ЎаSЎчABFЈҪSЎчAFCЈ¬
ЎаSЎчABFЈҪ![]() SЎчABCЈ¬
SЎчABCЈ¬
№Кҙр°ёОӘ![]() Ј®
Ј®
ОКМвМҪҫҝЈәЈЁ2Ј©ЎчABCЦРЈ¬УЙОКМвҪвҫцөДҪбВЫҝЙөГЈ¬SЎчBCDЈҪ![]() SЎчABCЈ¬SЎчBCEЈҪ
SЎчABCЈ¬SЎчBCEЈҪ![]() SЎчABCЈ®
SЎчABCЈ®
ЎаSЎчBCDЈҪSЎчBCE
ЎаSЎчBCD©ҒSЎчBOCЈҪSЎчBCE©ҒSЎчBOC
ЎаSЎчBODЈҪSЎчCOEЈ®
ЈЁ3Ј©ЎЯCDЈ¬BEЈ¬AF·ЦұрКЗЎчABCөДЦРПЯЈ¬
ЎаSЎчBOFЈҪSЎчCOFЈ¬ SЎчBAFЈҪSЎчCAFЈ¬SЎчBODЈҪSЎчAODЈ¬
АыУГМҪҫҝҪбВЫЈЁ1Ј©ЈЁ2Ј©ТЧЦӨЈәSЎчBOCЈҪSЛДұЯРОADOEЈ¬ SЎчBODЈҪSЎчCOE
ЎаSЎчAODЈҪSЎчBAFЈӯSЎчBODЈӯSЎчBOFЈҪSЎчCAFЈӯSЎчCOEЈӯSЎчCOFЈҪSЎчAOE
ЎаSЎчBOCЈҪ2SЎчBOFЈ¬SЛДұЯРОADOEЈҪ2SЎчAOD
ЎаSЎчBOFЈҪSЎчAOD
ЎаSЎчAOEЈҪSЎчAODЈҪSЎчBOFЈҪSЎчCOFЈҪSЎчBODЈҪSЎчCOEЈҪ![]() SЎчABCЈ¬
SЎчABCЈ¬
SЎчBOCЈҪ2SЎчBOFЈҪ![]() SЎчABCЈ¬SЎчAOEЈҪ
SЎчABCЈ¬SЎчAOEЈҪ![]() SЎчABCЈ¬SЎчBODЈҪ
SЎчABCЈ¬SЎчBODЈҪ![]() SЎчABFЈ®
SЎчABFЈ®
№Кҙр°ёОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
ОКМвНШХ№ЈәЈЁ4Ј©ўЩИзНј4ЦРЈ¬Б¬ҪУBDЈ®

ЎЯBEКЗЎчABDөДЦРПЯЈ¬
ЎаSЎчABEЈҪSЎчBDEЈ¬
ЎЯDFКЗЎчBCDөДЦРПЯЈ¬
ЎаSЎчBDFЈҪSЎчDFCЈ¬
ЎаSТхЈҪ![]() SЛДұЯРОABCDЈ¬
SЛДұЯРОABCDЈ¬
№Кҙр°ёОӘ![]() Ј®
Ј®
ўЪИзНј5ЦРЈ¬Б¬ҪУBDЈ¬ЙиBEҪ»DGУЪMЈ¬BHҪ»DFУЪNЈ®
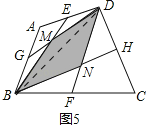
УГОКМвМҪҫҝҝЙЦӘЈәSЎчBDMЈҪ![]() SЎчABDЈ¬SЎчBDNЈҪ
SЎчABDЈ¬SЎчBDNЈҪ![]() SЎчBDCЈ¬
SЎчBDCЈ¬
ЎаSТхЈҪ![]() ЈЁSЎчABD+SЎчBDCЈ©ЈҪ
ЈЁSЎчABD+SЎчBDCЈ©ЈҪ![]() SЛДұЯРОABCDЈ¬
SЛДұЯРОABCDЈ¬
№Кҙр°ёОӘ![]() Ј®
Ј®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЖЛгПВБРёчМвЈә
(1) 4+(1)=___ Ј»(2) 3(2)=___Ј»(3)2ЎБ4=___Ј»(4)6ЎВ(2)=___Ј»(5)5+(1)2=___Ј»(6)1ЎВ3ЎБ![]() =___.
=___.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈәФЪЎчABCЦРЈ¬BEЎўCF·ЦұрКЗACЎўABБҪұЯЙПөДёЯЈ¬ФЪBEЙПҪШИЎBD=ACЈ¬ФЪCFөДСУіӨПЯЙПҪШИЎCG=ABЈ¬Б¬ҪУADЎўAGЈ®
ЈЁ1Ј©ЗуЦӨЈәAD=AGЈ»
ЈЁ2Ј©ADУлAGөДО»ЦГ№ШПөИзәОЈ¬ЗлЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝУР20ҝр°ЧІЛЈ¬ТФГҝҝр30З§ҝЛОӘұкЧјЈ¬і¬№э»тІ»ЧгөД·ЦұрУГХэЎўёәАҙұнКҫЈ¬јЗВјИзПВЈә
УлұкЧјЦКБҝөДІо(өҘО»ЈәЗ§ҝЛ) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
ҝрКэ | 1 | 4 | 2 | 3 | 2 | 8 |
ЈЁ1Ј©20ҝр°ЧІЛЦРЈ¬ЧоЦШөДТ»ҝрұИЧоЗбөДТ»ҝрТӘЦШ¶аЙЩЗ§ҝЛ?
ЈЁ2Ј©УлұкЧјЦКБҝұИҪПЈ¬20ҝр°ЧІЛЧЬјЖі¬№э»тІ»Чг¶аЙЩЗ§ҝЛ?
ЈЁ3Ј©Иф°ЧІЛГҝЗ§ҝЛКЫјЫ2ФӘЈ¬ФтіцКЫХв20ҝр°ЧІЛҝЙВф¶аЙЩФӘ?
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј1Ўў2Ј¬ТСЦӘЛДұЯРОABCDОӘХэ·ҪРОЈ¬ФЪЙдПЯACЙПУРТ»¶ҜөгPЈ¬ЧчPEЎНADЈЁ»тСУіӨПЯЈ©УЪEЈ¬ЧчPFЎНDCЈЁ»тСУіӨПЯЈ©УЪFЈ¬ЧчЙдПЯBPҪ»EFУЪGЈ®
ЈЁ1Ј©ФЪНј1ЦРЈ¬ЙиХэ·ҪРОABCDөДұЯіӨОӘ2Ј¬ЛДұЯРОABFEөДГж»эОӘyЈ¬AP=xЈ¬Зуy№ШУЪxөДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©ҪбВЫЈәGBЎНEF¶ФНј1Ј¬Нј2¶јКЗіЙБўөДЈ¬ЗлИОСЎТ»НјРОёшіцЦӨГчЈ»
ЈЁ3Ј©ЗлёщҫЭНј2ЦӨГчЈәЎчFGCЎЧЎчPFBЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
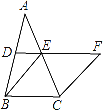
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬DЎўE·ЦұрКЗABЎўACөДЦРөгЈ¬BE=2DEЈ¬СУіӨDEөҪөгFЈ¬К№өГEF=BEЈ¬Б¬ҪУCFЈ®
ЈЁ1Ј©ЗуЦӨЈәЛДұЯРОBCFEКЗБвРОЈ»
ЈЁ2Ј©ИфCE=4Ј¬ЎПBCF=120ЎгЈ¬ЗуБвРОBCFEөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬Т»·Ҫ¶УХэСШјэН·ЛщЦёөД·ҪПтЗ°Ҫш

ЈЁ1Ј©AөДО»ЦГОӘөЪИэБРөЪЛДРРЈ¬ұнКҫОӘЈЁ3Ј¬4Ј©Ј¬ДЗГҙBөДО»ЦГКЗ____________Ј®
AЈ®![]() BЈ®
BЈ®![]() CЈ®
CЈ®![]() DЈ®
DЈ®![]()
ЈЁ2Ј©BЧуІаөЪ¶юёцИЛөДО»ЦГКЗ____________Ј®
AЈ®![]() BЈ®
BЈ®![]() CЈ®
CЈ®![]() DЈ®
DЈ®![]()
ЈЁ3Ј©Из№ы¶УОйПт¶«З°ҪшЈ¬ДЗГҙAұұІаөЪ¶юёцИЛөДО»ЦГКЗ____________Ј®
AЈ®![]() BЈ®
BЈ®![]() CЈ®
CЈ®![]() DЈ®
DЈ®![]()
ЈЁ4Ј©![]() ұнКҫөДО»ЦГКЗ____________Ј®
ұнКҫөДО»ЦГКЗ____________Ј®
AЈ®A BЈ®B CЈ®C DЈ®D
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРЈ¬ұЯABөДіӨОӘ3Ј¬өгEЈ¬F·ЦұрФЪADЈ¬BCЙПЈ¬Б¬ҪУBEЈ¬DFЈ¬EFЈ¬BDЈ®ИфЛДұЯРОBEDFКЗБвРОЈ¬ЗТEFЈҪAE+FCЈ¬ФтұЯBCөДіӨОӘЈЁЎЎЎЎЈ©

A. 2![]() B. 3
B. 3![]() C. 6
C. 6![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,ФЪЎчABCЦР,ЎПC=90Ј¬AC=BCЈ¬ADЖҪ·ЦЎПCABЈ¬DEЎНABЈ¬ҙ№ЧгОӘE.
(1)ЗуЦӨЈәCD=BEЈ»
(2)ИфAB=10Ј¬ЗуBDөДіӨ¶ИЎЈ

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com