
【题目】如图,平行四边形ABCD的边AB在x轴上,点C的坐标为(﹣5,4),点D在y轴的正半轴上,经过点A的直线y=![]() x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
x﹣1与y轴交于点E,将直线AE沿y轴向上平移n(n>0)个单位长度后,得到直线l,直线l经过点C时停止平移.
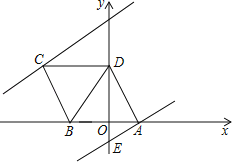
(1)点A的坐标为 ,点B的坐标为 ;
(2)若直线l交y轴于点F,连接CF,设△CDF的面积为S(这里规定:线段是面积为0的三角形),求S与n之间的函数关系式,并写出n的取值范围;
(3)易知AE⊥AD于点A,若直线l交折线AD﹣DC于点P,当△AEP为直角三角形时,请直接写出n的取值范围.
【答案】(1)A(2,0),B(-3,0);(2)当0≤n≤5时,S=10-2n;当5<n≤![]() 时,S=2n-10;(3)n=
时,S=2n-10;(3)n=![]() 或0≤n≤5.
或0≤n≤5.
【解析】
(1)令y=0,则![]() x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
x-1=0,求A(2,0),由平行四边形的性质可知AB=5,则B(-3,0);
(2)易求E(0,-1),当l到达C点时的解析式为y=![]() x+
x+![]() ,当0≤n≤5时,S=
,当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;当5<n≤
×4×(5-n)=10-2n;当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)由点可以得到AD⊥AE;当P在AD上时,△AEP为直角三角形,0≤n≤5;当P在CD上时,△AEP为直角三角形,则PE⊥AE,设P(m,4),可得![]() =-2,求出P(-
=-2,求出P(-![]() ,4),此时l的解析式为y=
,4),此时l的解析式为y=![]() x+
x+![]() ,则n=
,则n=![]() .
.
(1)令y=0,则![]() x-1=0,x=2,
x-1=0,x=2,
∴A(2,0),
∵C的坐标为(-5,4),四边形ABCD是平行四边形,
∴AB=CD=5,
∴OB=AB-OA=3,∴B(-3,0);
(2)当x=0时,y=![]() x﹣1=-1,所以E(0,-1),
x﹣1=-1,所以E(0,-1),
∵直线AE沿y轴向上平移得到l,当l到达C点时的解析式为y=![]() x+
x+![]() ,
,
此时l与y轴的交点为(0,![]() ),
),
当0≤n≤5时,S=![]() ×4×(5-n)=10-2n;
×4×(5-n)=10-2n;
当5<n≤![]() 时,S=
时,S=![]() ×4×(n-5)=2n-10;
×4×(n-5)=2n-10;
(3)∵D(0,4),A(2,0),E(0,-1),
∴AD=2![]() ,AE=
,AE=![]() ,ED=5,
,ED=5,
∴AD2+AE2=ED2,
∴AD⊥AE,
当P在AD上时,△AEP为直角三角形,
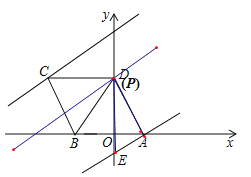
∴0≤n≤5;
当P在CD上时,△AEP为直角三角形,
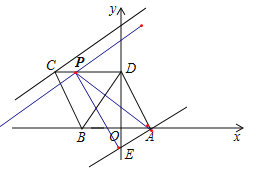
则PE⊥AE,
设P(m,4),
∴![]() =-2,
=-2,
∴m=-![]() ,
,
∴P(-![]() ,4),
,4),
∴此时l的解析式为y=![]() x+
x+![]() ,
,
∴n=![]() ;
;
综上所述:当△AEP为直角三角形时,n=![]() 或0≤n≤5.
或0≤n≤5.


科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
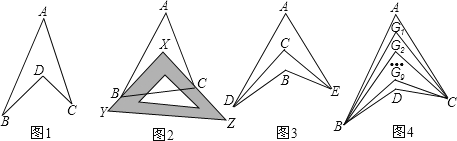
如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有理数 a,b,c 分别对应数轴上的点 A,B,C,若a 2![]() |b 4| 0 ,关于 x、y 的单项式3(c 3)x
|b 4| 0 ,关于 x、y 的单项式3(c 3)x![]() y
y![]() 与 y
与 y![]() x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
x 是同类项. 我们把数轴上两点之间的距离用表示两点的大写字母一起标记,例如,点 A 与点 B 间的距离记作 AB.
![]()
![]()
(1)求 a,b,c 的值;
(2)点 P 从 C 点出发以每秒 1 个单位长度在数轴上按以下规律往返运动:第一回合,从点 C 到点 B 到点 A 回到点 C;第二回合,从点 C 到 BC 的中点 D 到 CA 的中点 D1 回到点 C;第三回合,从点 C 到 CD 的中点 D2 到 CD1 的中点 D3 回到点 C……,如此循环下去,若第 t 秒时满足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的条件下,P 点第一次从 C 点出发的同时,数轴上的动点 M、N 分别从 A 点和 B 点向右运动,速度分别为每秒 1 个单位长度和每秒 2 个单位长度,P 点完成第一个回合后停止在 C 点,当 MP=2MN 时, t 的值是 (直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A对应的数是-6,点B对应的数是-2,点O对应的数是0.动点P、Q分别从A、B同时出发,以每秒3个单位,每秒1个单位的速度向右运动。在运动过程中,线段PQ的长度始终是另一线段长的整数倍,这条线段是( )

A.PBB.OPC.OQD.QB
查看答案和解析>>
科目:初中数学 来源: 题型:
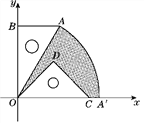
【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3![]() .
.
(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
【答案】(1)反比例函数的解析式为y=![]() ;(2)S阴影=6π-
;(2)S阴影=6π-![]() .
.
【解析】分析:(1)根据tan30°=![]() ,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=
,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=![]() ,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
本题解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴点A的坐标为(3,3![]() ).
).
设反比例函数的解析式为y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,则这个反比例函数的解析式为y=
,则这个反比例函数的解析式为y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由题意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S阴影=S扇形AOA′-S△ODC=6π-![]() .
.
点睛:本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质,本题属于中档题,难度不大,将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
26
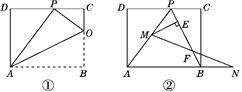
【题目】矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O,连接AP,OP,OA.
① 求证:△OCP∽△PDA;
② 若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
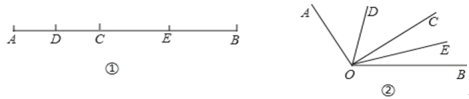
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com