
【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:
月均用水量 | 频数 | 频率 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 |
| 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 |
|
25≤x<30 | 2 | 4% |
合计 |
| 100% |
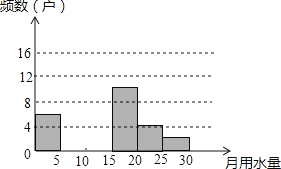
请解答以下问题:
(I)把上面的频数分布表和频数分布直方图补充完整;
(Ⅱ)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(Ⅲ)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
【答案】(I)详见解析;(Ⅱ)240;(Ⅲ)15t.
【解析】
(Ⅰ)由0≤x<5的频数及其频率可得总户数,再根据频率=频数÷总户数分别求解可得;
(Ⅱ)用总户数乘以样本中20≤x<25、25≤x<30的频率和即可得;
(Ⅲ)前三个分组的频率之和为12%+24%+32%=68%即可得.
(Ⅰ)∵被调查的总数量为6÷12%=50(户),
∴10≤x<15的频数为50×32%=16(户)、20≤x<25的频率为4÷50=0.08=8%,
补全图形如下:
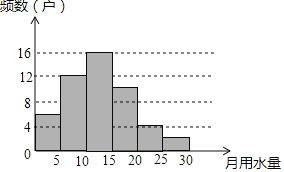
月均用水量 | 频数 | 频率 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 | 16 | 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 | 8% |
25≤x<30 | 2 | 4% |
合计 | 50 | 100% |
(Ⅱ)估计该小区月均用水量不低于20t的家庭有2000×(8%+4%)=240户;
(Ⅲ)∵前三个分组的频率之和为12%+24%+32%=68%,
∴家庭月均用水量应定为15t.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转45°后得到正方形
逆时针旋转45°后得到正方形![]() .依此方式,绕点
.依此方式,绕点![]() 连续旋转2020次,得到正方形
连续旋转2020次,得到正方形![]() ,如果点
,如果点![]() 的坐标为
的坐标为![]() ,那么点
,那么点![]() 的坐标为( )
的坐标为( )
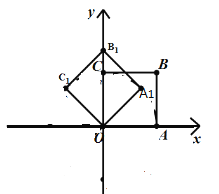
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
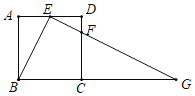
【题目】如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足a+b+c=0,我们称这个方程为“凤凰”方程.已知
满足a+b+c=0,我们称这个方程为“凤凰”方程.已知![]() 是凤凰方程,且有两个相等的实数根,则下列正确的是( )
是凤凰方程,且有两个相等的实数根,则下列正确的是( )
A.a=cB.a=bC.b=cD.a=b=c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆D的直径AB=4,线段OA=7,O为原点,点B在数轴的正半轴上运动,点B在数轴上所表示的数为m.
(1)当半圆D与数轴相切时,m= .
(2)半圆D与数轴有两个公共点,设另一个公共点是C.
①直接写出m的取值范围是 .
②当BC=2时,求△AOB与半圆D的公共部分的面积.
(3)当△AOB的内心、外心与某一个顶点在同一条直线上时,求tan∠AOB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
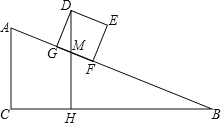
【题目】某仓储中心有一个坡度为i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE=2.5米,高EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(-5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点.
(1)求b的值;
(2)将二次函数y=2x2+bx+1的图象进行一次平移,使图象经过原点.(写出一种即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com