
【题目】已知抛物线y=x2-2bx+c.
(1)若抛物线的顶点坐标为(2,-3),求b,c的值;
(2)若b+c=0,是否存在实数x,使得相应的y的值为1?请说明理由;
(3)若c=b+2且抛物线在-2≤x≤2上的最小值是-3,求b的值.
【答案】(1)b=2,c=1(2)存在(3)3或![]()
【解析】
(1)根据题意得到抛物线为y=(x-2)2-3,整理成一般式即可求得b,c的值;
(2)令y=1,判断所得方程的判别式大于0即可求解;
(3)求得函数的对称轴是x=b,然后分成b≤-2,-2<b<2和b≥2三种情况进行讨论,然后根据最小值是-3,即可解方程求解.
解:(1)∵抛物线y=x2-2bx+c,
∴a=1.
∵抛物线的顶点坐标为(2,-3),
∴y=(x-2)2-3.
∵y=(x-2)2-3=x2-4x+1,
∴b=2,c=1.
(2)存在.
理由:由y=1,得x2-2bx+c=1,
∴x2-2bx+c-1=0.
∵Δ=4b2+4b+4=(2b+1)2+3>0,
则存在两个实数x,使得y=1.
(3)由c=b+2,则抛物线可化为y=x2-2bx+b+2,其对称轴为直线x=b.
①当b≤-2时,则抛物线在x=-2时取得最小值,此时
-3=(-2)2-2×(-2)b+b+2,
解得b=-![]() ,不合题意;
,不合题意;
②当b≥2时,则抛物线在x=2时取得最小值,
此时-3=22-2×2b+b+2,
解得b=3;
③当-2<b<2时,则抛物线在x=b时取得最小值,
此时![]() =-3,
=-3,
化简,得b2-b-5=0,
解得b1=![]() (不符合题意,舍去),b2=
(不符合题意,舍去),b2=![]() .
.
综上所述,b的值为3或![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=8,FC=6.
(1)求EF的长.
(2)求四边形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
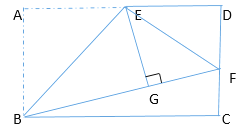
【题目】如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,连接EF,若AB=4,若BC=6,则DF的长为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,点A、B的坐标分别是A(-1,0),B(3,0),将线段AB向上平移2个单位,再向右平移1个单位,得到线段DC,点A、B的对应点分别是D、C,连接AD、BC.
(1)直接写出点C,D的坐标;
(2)求四边形ABCD的面积;
(3)点P为线段BC上任意一点(与点B、C不重合),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 y=ax2+bx﹣![]() 与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
(1)求此抛物线的解析式;
(2)若 E 点在第一象限,过点 E 作 EF⊥x 轴于点 F,△ADO 与△AEF 的面积比为![]() =
=![]() ,求出点 E 的坐标;
,求出点 E 的坐标;
(3)若 D 是 y 轴上的动点,过 D 点作与 x 轴平行的直线交抛物线于 M、N 两点, 是否存在点 D,使 DA2=DMDN?若存在,请求出点 D 的坐标;若不存在,请说 明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com