
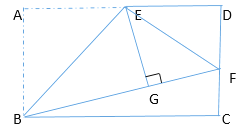
【题目】如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,连接EF,若AB=4,若BC=6,则DF的长为_______ .
科目:初中数学 来源: 题型:
【题目】如图是考古学家发现的古代钱币的一部分,合肥一中的小明正好学习了圆的知识,他想求其外圆半径,连接外圆上的两点A,B,并使AB与内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10 cm,AB=60 cm,则这个钱币的外圆半径为__cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,已知数
,已知数![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数 表示的点重合;
与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() 、
、![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示);
的式子表示);
(4)在(3)的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某街区的平面示意图,根据要求答题.

(1)这幅图的比例尺是( )
(2)学校位于广场的( )面(填东、南、西、北)( )千米处.
(3)人民公园位于广场的东偏南![]() 方向3千米处.在图中标出它的位置.
方向3千米处.在图中标出它的位置.
(4)广场的西面1千米处,有一条商业街与人民路垂直,在图中画线表示商业街.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-2bx+c.
(1)若抛物线的顶点坐标为(2,-3),求b,c的值;
(2)若b+c=0,是否存在实数x,使得相应的y的值为1?请说明理由;
(3)若c=b+2且抛物线在-2≤x≤2上的最小值是-3,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
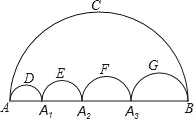
【题目】图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A. 甲先到B点 B. 乙先到B点 C. 甲、乙同时到B D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在平面直角坐标系中S△ABC=24,OA=OB,BC=12.

(1)求出三个顶点坐标.
(2)若P点为y轴上的一动点,且△ABP的面积等于△ABC的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0.
(1)判断方程根的情况;
(2)若方程的两根x1,x2满足(x1-1)(x2-1)=5,求k值;
(3)若△ABC的两边AB,AC的长是方程的两根,第三边BC的长为5,
①则k为何值时,△ABC是以BC为斜边的直角三角形?
②k为何值时,△ABC是等腰三角形,并求出△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com