
【题目】已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
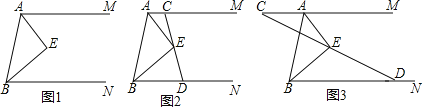
(1)求![]() 的度数;
的度数;
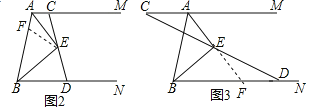
(2)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,过点![]() 的直线交射线
的直线交射线![]() 的反向延长线于点
的反向延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)90°;(2)见解析;(3)8
【解析】
(1)根据平行线的性质得到∠BAM+∠ABN=180°,根据角平分线的定义得到∠BAE=![]() ∠BAM,∠ABE=
∠BAM,∠ABE=![]() ∠ABN,于是得到结论;
∠ABN,于是得到结论;
(2)在AB上截取AF=AC,连接EF,根据全等三角形的性质得到∠AEC=∠AEF,BF=BD,等量代换即可得到结论;
(3)延长AE交BD于F,根据等腰三角形的性质得到AB=BF=5,AE=EF,根据全等三角形的性质得到DF=AC=3,设S△BEF=S△ABE=5x,S△DEF=S△ACE=3x,根据S△ABE-S△ACE=2,即可得到结论.
解:(1)∵AM∥BN,
∴∠BAM+∠ABN=180°,
∵AE平分∠BAM,BE平分∠ABN,
∴∠BAE=![]() ∠BAM,∠ABE=
∠BAM,∠ABE=![]() ∠ABN,
∠ABN,
∴∠BAE+∠ABE=![]() (∠BAM+∠ABN)=90°,
(∠BAM+∠ABN)=90°,
∴∠AEB=90°;
(2)在AB上截取AF=AC,连接EF,
在△ACE与△AFE中,
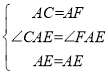 ,
,
∴△ACE≌△AFE,
∴∠AEC=∠AEF,
∴∠AEB=90°,
∴∠AEF+∠BEF=∠AEC+∠BED=90°,
∴∠FEB=∠DEB,
在△BFE与△BDE中,
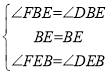 ,
,
∴△BFE≌△BDE(ASA),
∴BF=BD,
∵AB=AF+BF,
∴AC+BD=AB;
(3)延长AE交BD于F,
∵∠AEB=90°,
∴BE⊥CD,
BE平分∠ABN,
∴AB=BF=5,AE=EF,
∵AM∥BN,
∴∠C=∠EDF,
在△ACE与△FDE中,
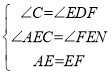 ,
,
∴△ACE≌△FDE(AAS),
∴DF=AC=3,
∵BF=5,
∴设S△BEF=S△ABE=5x,S△DEF=S△ACE=3x,
∵S△ABE-S△ACE=2,
∴5x-3x=2,
∴x=1,
∴△BDE的面积=8.


科目:初中数学 来源: 题型:
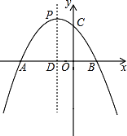
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
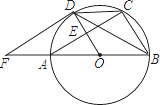
【题目】如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
(1)他们在一次实验中共做了![]() 次试验,试验的结果如下:
次试验,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最小.”她的说法正确吗?为什么?
点朝上的概率最小.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0
(Ⅰ)当m=![]() 时,求方程的实数根;
时,求方程的实数根;
(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华有一个容最为8![]() (
(![]() )的
)的![]() 盘,
盘,![]() 盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间
盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间![]() 与图片数量
与图片数量![]() (张)满足一次函数关系,对应数据如下表:
(张)满足一次函数关系,对应数据如下表:
图片数量 | 100 | 150 |
剩余可用空间 | 5700 | 5550 |
(1)求出![]() 与
与![]() 之间的关系式,并求出
之间的关系式,并求出![]() 盘中视频文件占用的内存容量;
盘中视频文件占用的内存容量;
(2)若![]() 盘中已经存入1280张照片,那么最多还能存入多少张照片?
盘中已经存入1280张照片,那么最多还能存入多少张照片?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com