
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
(1)他们在一次实验中共做了![]() 次试验,试验的结果如下:
次试验,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最小.”她的说法正确吗?为什么?
点朝上的概率最小.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
【答案】(1)①![]() ;②小红的说法不正确,理由详见解析;(2)
;②小红的说法不正确,理由详见解析;(2)![]() .
.
【解析】
(1)用出现3的次数除总次数即可得解;
(2)小红的说法不正确,利用频率估计概率实验次数必须比较多,重复实验,频率才慢慢接近概率,而她的实验次数太少,没有代表性;
(3)根据题意画树状图,然后用概率公式求得出现次数最多的情况概率即可.
解:(1)①∵实验中“![]() 点朝上”的次数有
点朝上”的次数有![]() 次,总数为
次,总数为![]() ,
,
∴此次实验中“![]() 点朝上”的频率为
点朝上”的频率为![]() ;
;
②小红的说法不正确,
∵利用频率估计概率实验次数必须比较多,重复实验,频率才慢慢接近概率,而她的实验次数太少,没有代表性,
∴小红的说法不正确;
(2)两枚骰子朝上的点数之和可能情况:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
,
![]() ,
,
![]() ,
,
∴和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
和为![]() 的有
的有![]() 种,
种,
两枚骰子朝上的点数之和为![]() 时的概率最大,
时的概率最大,
则最大概率为:![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中装有四个完全相同的小球,它们分别写有“美”“丽”、“黄”、“石”的文字.
(1)先从袋摸出![]() 个球后放回,混合均匀后再摸出
个球后放回,混合均匀后再摸出![]() 个球,求两次摸出的球上是写有“美丽”二字的概率;
个球,求两次摸出的球上是写有“美丽”二字的概率;
(2)先从袋中摸出![]() 个球后不放回,再摸出
个球后不放回,再摸出![]() 个球.求两次摸出的球上写有“黄石”二字的概率.
个球.求两次摸出的球上写有“黄石”二字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
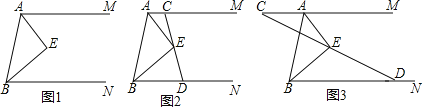
(1)求![]() 的度数;
的度数;
(2)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,过点![]() 的直线交射线
的直线交射线![]() 的反向延长线于点
的反向延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 两点分别位于一个池塘的两侧,池塘西南边有一座假山
两点分别位于一个池塘的两侧,池塘西南边有一座假山![]() ,在
,在![]() 的中点
的中点![]() 处有一个雕塑,小川从点
处有一个雕塑,小川从点![]() 出发,沿直线
出发,沿直线![]() 一直向前经过点
一直向前经过点![]() 走到点
走到点![]() ,并使
,并使![]() ,然后他测量点
,然后他测量点![]() 到假山
到假山![]() 的距离,则
的距离,则![]() 的长度就是
的长度就是![]() 、
、![]() 两点之间的距离.请根据题意完成下列问题:
两点之间的距离.请根据题意完成下列问题:
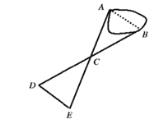
(1)题中给出的已知条件是什么?
已知:_______________________________________________________;
(2)得出的结论是什么?
结论:______________________________________________________;
(3)根据题意写出证明.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=2,△ABC的面积是3,那么这个正方形的边长是_________.
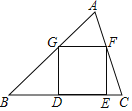
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com