
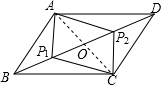
 如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.
如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.  开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
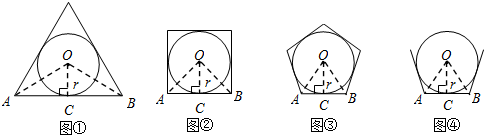
 如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?
如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-1)<-(+2) | B. | -$\frac{5}{6}>-\frac{5}{7}$ | C. | -(-5$\frac{1}{2}$)>|-5.5| | D. | -$\frac{7}{8}$$<-\frac{6}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
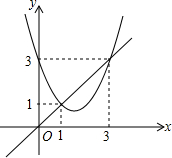 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 某种彩票中奖的概率是1%,因此买100张该彩票一定会中奖 | |
| B. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| C. | 一个袋中装有3个红球、5个白球,任意摸出一个球是红球的概率是$\frac{3}{5}$ | |
| D. | 抛掷两枚普通的硬币,两枚硬币均出现正面向上的概率是25% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com