
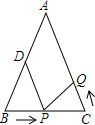
 如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.分析 (1)根据路程=速度×时间就可以得出结论;
(2)当BP=PC时,BD=CQ,由BP+CP=BC=8,得出BP=4,t=$\frac{4}{3}$s CQ=4不成立;
当BP=CQ时,BD=CP,由中点的定义得出BD=AD=5,CP=5,BP=3,即可得出结果;
(3)设Q的速度为acm/s,则P的速度为(a-1)cm/s,由BP与CQ不相等,得出BD=CQ,BP=CP,设运动时间为ts,则at=5,(a-1)t=4,解得t=1s,a=5cm/s即可.
解答 解:(1)∵由题意得:BP=3t,
∴PC=8-3t;
故答案为:3t,8-3t;
(2)经过1秒钟△BPD与△CQP全等,理由如下:
当BP=PC时,BD=CQ,
∵BP+CP=BC=8,
∴BP=4,
∴t=$\frac{4}{3}$s CQ=4不成立;
当BP=CQ时,BD=CP,
∵点D为AB的中点,
∴BD=AD,
∵AB=10,
∴BD=5,
∴CP=5,
∴BP=3,
∴t=1,故t=1;
即若点Q运动速度与点P的运动速度相等,经过1秒钟△BPD与△CQP全等;
(3)设Q的速度为acm/s,则P的速度为(a-1)cm/s,
∵BP与CQ不相等,
∴BD=CQ,BP=CP,
设运动时间为ts,
∴at=5,(a-1)t=4,
∴t=1s,a=5cm/s;
即Q的速度是5cm/s时,△BPD≌△CQP.
点评 本题考查了全等三角形的判定的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
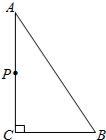 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
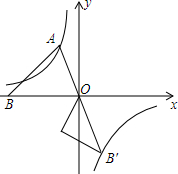 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
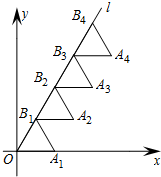 如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).
如图,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标为(1008,1007$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com