
،¾جâؤ؟،؟ؤ³حّµêدْتغز»ضض¶ùح¯حو¾ك£¬½ّ¼غخھأ؟¼30شھ£¬خï¼غ²؟أإ¹و¶¨أ؟¼¶ùح¯حو¾كµؤدْتغہûبَ²»¸كسع½ّ¼غµؤ![]() £®شعدْتغ¹³جضذ·¢دض£¬صâضض¶ùح¯حو¾كأ؟جىµؤدْتغء؟
£®شعدْتغ¹³جضذ·¢دض£¬صâضض¶ùح¯حو¾كأ؟جىµؤدْتغء؟![]() £¨¼
£¨¼![]() سëدْتغµ¥¼غ
سëدْتغµ¥¼غ![]() £¨شھ
£¨شھ![]() آْ×مز»´خ؛¯ت¹طدµ£®µ±دْتغµ¥¼غخھ35شھت±£¬أ؟جىµؤدْتغء؟خھ350¼£»µ±دْتغµ¥¼غخھ40شھت±£¬أ؟جىµؤدْتغء؟خھ300¼£®
آْ×مز»´خ؛¯ت¹طدµ£®µ±دْتغµ¥¼غخھ35شھت±£¬أ؟جىµؤدْتغء؟خھ350¼£»µ±دْتغµ¥¼غخھ40شھت±£¬أ؟جىµؤدْتغء؟خھ300¼£®
£¨1£©اَ![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµت½£®
ض®¼نµؤ؛¯ت¹طدµت½£®
£¨2£©µ±دْتغµ¥¼غخھ¶àةظت±£¬¸أحّµêدْتغصâضض¶ùح¯حو¾كأ؟جى»ٌµأµؤہûبَ×î´َ£¬×î´َہûبَتا¶àةظ£؟
،¾´ً°¸،؟£¨1£©![]() £»£¨2£©µ±دْتغµ¥¼غخھ48شھت±£¬¸أحّµêدْتغصâضض¶ùح¯حو¾كأ؟جى»ٌµأµؤہûبَ×î´َ£¬×î´َہûبَتا3960شھ£®
£»£¨2£©µ±دْتغµ¥¼غخھ48شھت±£¬¸أحّµêدْتغصâضض¶ùح¯حو¾كأ؟جى»ٌµأµؤہûبَ×î´َ£¬×î´َہûبَتا3960شھ£®
،¾½âخِ،؟
£¨1£©ةè![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµت½خھ
ض®¼نµؤ؛¯ت¹طدµت½خھ![]() £¬¸ù¾فجâزâµأµ½·½³ج×飬سعتاµأµ½½لآغ£»
£¬¸ù¾فجâزâµأµ½·½³ج×飬سعتاµأµ½½لآغ£»
£¨2£©ةèہûبَخھ![]() شھ£¬ءذ²»µبت½µأµ½
شھ£¬ءذ²»µبت½µأµ½![]() £¬¸ù¾فجâزâµأµ½؛¯ت½âخِت½
£¬¸ù¾فجâزâµأµ½؛¯ت½âخِت½![]() £¬¸ù¾ف¶´خ؛¯تµؤذشضت¼´؟ةµأµ½½لآغ£®
£¬¸ù¾ف¶´خ؛¯تµؤذشضت¼´؟ةµأµ½½لآغ£®
£¨1£©ةè![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµت½خھ
ض®¼نµؤ؛¯ت¹طدµت½خھ![]() £¬
£¬
¸ù¾فجâزâµأ£¬![]() £¬
£¬
½âµأ£؛![]() £¬
£¬
![]() سë
سë![]() ض®¼نµؤ؛¯ت¹طدµت½خھ
ض®¼نµؤ؛¯ت¹طدµت½خھ![]() £»
£»
£¨2£©ةèہûبَخھ![]() شھ£¬
شھ£¬
![]() £¬
£¬
![]() £¬
£¬
¸ù¾فجâزâµأ£¬![]() £¬
£¬
![]() £¬¶ش³ئضل
£¬¶ش³ئضل![]() £¬
£¬
![]() µ±
µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
´ً£؛µ±دْتغµ¥¼غخھ48شھت±£¬¸أحّµêدْتغصâضض¶ùح¯حو¾كأ؟جى»ٌµأµؤہûبَ×î´َ£¬×î´َہûبَتا3960شھ£®


 ؛®¼ظر§سëء·دµءذ´ً°¸
؛®¼ظر§سëء·دµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعز»¸ِ²»ح¸أ÷µؤ؟ع´üہï×°سذض»سذرصة«²»ح¬µؤ؛ع،¢°×ء½ضضرصة«µؤاٍ¹²10ض»£¬ؤ³ر§د°ذ،×é×ِأاٍتµر飬½«اٍ½ءشب؛َ´سضذثو»ْأ³ِز»¸ِاٍ¼ادآرصة«£¬شظ°رثü·إ»ط´üضذ£¬²»¶دضط¸´£®دآ±يتا»î¶¯½ّذذضذµؤز»×éح³¼ئت¾ف£؛
أاٍµؤ´خت | 100 | 150 | 200 | 500 | 800 | 1000 |
أµ½°×اٍµؤ´خت | 58 | 96 | 116 | 295 | 484 | 601 |
أµ½°×اٍµؤئµآت | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
£¨1£©اë¹ہ¼ئ£؛µ±![]() ؛ـ´َت±£¬أµ½°×اٍµؤئµآت½«»ل½س½ü،، ،،£»£¨±£ءô¶¸ِسذذ§ت×ض£©
؛ـ´َت±£¬أµ½°×اٍµؤئµآت½«»ل½س½ü،، ،،£»£¨±£ءô¶¸ِسذذ§ت×ض£©
£¨2£©تش¹ہثم؟ع´üضذ؛ع،¢°×ء½ضضرصة«µؤاٍ¸÷سذ¶àةظض»£؟
£¨3£©اë»ت÷×´ح¼»ٍءذ±ي¼ئثم£؛´سضذز»´خأء½ض»اٍ£¬صâء½ض»اٍرصة«²»ح¬µؤ¸إآتتا¶àةظ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬½«ءâذخض½ئ¬ABCDصغµ£¬ت¹µمAا،؛أآنشعءâذخµؤ¶ش³ئضذذؤO´¦£¬صغ؛غخھEF£¬بôءâذخABCDµؤ±ك³¤خھ2cm£¬،دA=120،م£¬شٍEFµؤ³¤خھ£¨،،،،£©
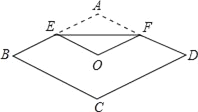
A. 2![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعABCDضذ£¬،دBADµؤئ½·ضدك½»ض±دكBCسعµمE£¬½»ض±دكDCسعµمF£®
£¨1£©شعح¼1ضذض¤أ÷CE=CF£»
£¨2£©بô،دABC=90،م£¬GتاEFµؤضذµم£¨بçح¼2£©£¬ض±½سذ´³ِ،دBDGµؤ¶بت£»
£¨3£©بô،دABC=120،م£¬FG،خCE£¬FG=CE£¬·ض±ًء¬½سDB،¢DG£¨بçح¼3£©£¬اَ،دBDGµؤ¶بت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
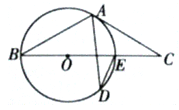
،¾جâؤ؟،؟بçح¼£¬BEتا،رOµؤض±¾¶£¬µمA؛حµمDتا،رOةدµؤء½µم£¬¹µمA×÷،رOµؤاذدك½»BEرس³¤دكسعµمC
£¨I£©بô،دADE=25،م£¬اَ،دCµؤ¶بت
£¨II£©بôAB=AC£¬اَ،دDµؤ¶بت.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
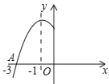
،¾جâؤ؟،؟بçح¼تا¶´خ؛¯تy£½ax2+bx+cµؤح¼دَµؤز»²؟·ض£¬ح¼دَ¹µمA£¨©پ3£¬0£©£¬¶ش³ئضلتاض±دكx£½©پ1£¬¸ّ³ِخه¸ِ½لآغ£؛¢ظb2£¾4ac£»¢ع2a©پb£½0£»¢غc£¼0£»¢ـa+b+c£½0£»¢فa©پb+c£¼0£®ئنضذصب·µؤتا____£¨°رؤمبدخھصب·µؤذٍ؛إ¶¼جîةد£©£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دضسذز»¶خ120mµؤہé°ت£¬×¼±¸سأصâذ©ہé°ت½èضْز»¶خا½½اخ§³ةبçح¼ثùت¾ء½؟éأو»دàح¬µؤ¾طذخ³،µطرّ¼¦.
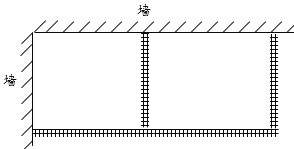
£¨1£©بçح¼ثùت¾£¬بôخ§³ةµؤ³،µط×ـأو»خھ1750m2£¬شٍ¸أ³،µطµؤ؟ي£¨ح¼ضذ×فدٍ£©س¦خھ¶àةظ£؟
£¨2£©ؤـ²»ؤـخ§³ةأو»خھ2000m2µؤ³،µط£؟بôؤـ£¬اَ³ِ´ثت±ہé°تµؤ؟ي£»بô²»ؤـ£¬اَخ§³ة³،µطأو»µؤ×î´َضµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼تاز»¸ِسأہ´ت¢±¬أ×»¨µؤش²×¶ذخض½±,ض½±؟ھ؟عµؤض±¾¶ EF ³¤خھ10cm,ؤ¸دكOE(OF)³¤خھ10cm,شعؤ¸دكOF ةدµؤµمA ´¦سذز»؟鱬أ×»¨²ذشüازFA£½2cm,ز»ض»آىزد´س±؟عµؤµمE ´¦رطش²×¶±يأوإہذذµ½A µم,شٍ´ثآىزدإہذذµؤ×î¶ج¾àہëخھ cm£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
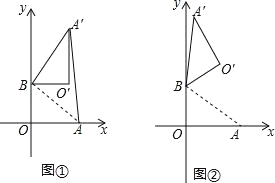
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµضذ£¬O خھشµم£¬µم A£¨4£¬0£©£¬µم B£¨0£¬3£©£¬°ر،÷ABO بئµم B ؤوت±صëذ×ھ£¬µأ،÷A،نBO،ن£¬µم A،¢O ذ×ھ؛َµؤ¶شس¦µمخھ A،ن،¢O،ن£¬¼اذ×ھ½اخھ¨»£®
(1)بçح¼ 1£¬بô¨»£½90،م£¬اَ AA،نµؤ³¤£»
(2)بçح¼ 2£¬بô¨»£½120،م£¬اَµم O،نµؤ×ّ±ê£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com