

分析 根据题意容易得出AB和CD的长;连接OB,设半径CO=OB=x寸,先根据垂径定理求出CA的长,再根据勾股定理求出x的值,即可得出直径.
解答 解:根据题意得:AB=1寸,CD=10寸;
故答案为:1,10;
(2)连接CO,如图所示: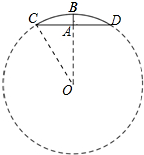
∵BO⊥CD,
∴$CA=\frac{1}{2}CD=5$.
设CO=OB=x寸,则AO=(x-1)寸,
在Rt△CAO中,∠CAO=90°,
∴AO2+CA2=CO2.
∴(x-1)2+52=x2.
解得:x=13,
∴⊙O的直径为26寸.
点评 本题考查了勾股定理在实际生活中的应用;根据题意作出辅助线,构造出直角三角形,运用勾股定理得出方程是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com