
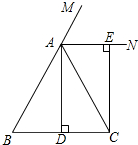
 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠ACM的平分线,CE⊥AN,垂足为点E
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠ACM的平分线,CE⊥AN,垂足为点E分析 (1)由在△ABC中,AB=AC,AD是BC边的中线,可得AD⊥BC,∠BAD=∠CAD,又由AN为△ABC的外角∠CAM的平分线,可得∠DAE=90°,又由CE⊥AN,即可证得:四边形ADCE为矩形;
(2)根据正方形的判定,我们可以假设当AD=$\frac{1}{2}$BC,由已知可得,DC=$\frac{1}{2}$BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
解答 (1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)当△ABC满足∠BAC=90°时,四边形ADCE是正方形.
证明:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE是矩形,
∴矩形ADCE是正方形.
点评 本题是以开放型试题,主要考查了对矩形的判定,正方形的判定,等腰三角形的性质,及角平分线的性质等知识点的综合运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:选择题
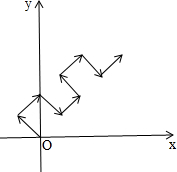 一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )
一个质点从原点开始在x轴上方按如图中箭头所示方向运动且每次运动相同的距离,第1次,它从原点运动到(-1,1),第2次从(-1,1)运动到(0,2),…,即:(0,0)→(-1,1)→(0,2)→(1,1)→(2,2)→(1,3)→(2,4)→(3,3)→…,那么质点第20次移动到达的位置的坐标是( )| A. | (9,11) | B. | (11,11) | C. | (10,10) | D. | (10,12) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 883.6×108 | B. | 8.836×108 | C. | 8.836×109 | D. | 8.836×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某高校共有5个一样规模的大餐厅和3个一样规模的小餐厅.经过测试:同时开放3个大餐厅、2个小餐厅,可供3300名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2100名学生就餐.
某高校共有5个一样规模的大餐厅和3个一样规模的小餐厅.经过测试:同时开放3个大餐厅、2个小餐厅,可供3300名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2100名学生就餐.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
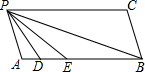 如图所示,已知PC∥AB,∠APC=∠ABC=80°,D、E在AB上,且满足∠BPC=∠BPE,∠APD=∠DPE.
如图所示,已知PC∥AB,∠APC=∠ABC=80°,D、E在AB上,且满足∠BPC=∠BPE,∠APD=∠DPE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com