
【题目】已知,在![]() 中,以
中,以![]() 、
、![]() 为边分别向形外作等边
为边分别向形外作等边![]() 和
和![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点.
中点.
(1)如图(a)所示,当![]() 时,
时,![]() 的度数为__________.
的度数为__________.
(2)如图(b)所示,当![]() 时,
时,![]() 的度数是否发生变化?证明你的结论.
的度数是否发生变化?证明你的结论.

【答案】(1)60°;(2)![]() 的度数不变,仍是60°,证明见解析.
的度数不变,仍是60°,证明见解析.
【解析】
(1)设AC中点G、BC中点H,连接MG、PG;NH,PH,利用中位线定理可以证明△MGP和△PHN全等,然后利用角之间的关系即可得出答案;
(2)由题意可知MF是等边△ACD的中位线,PG是△ABC的中位线,根据中位线的性质可知四边形CFPG是平行四边形,再根据平行四边形的性质可证明△MFP≌△PGN,即可得出答案.
解:(1)60°
取![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]()
又M是CD的中点,P是AB的中点,N是CE的中点
∴MG=![]() AD,MG∥AD,NH=
AD,MG∥AD,NH=![]() EB,NH∥EB ,GP=
EB,NH∥EB ,GP=![]() BC,GP∥BC ,HP =
BC,GP∥BC ,HP =![]() AC,HP∥AC
AC,HP∥AC
又∵△ACD和△ABE均为等边三角形
∴AD=AC,BC=BE,∠MGC=∠DAC=60°,∠CGP=∠ECB=60°, ∠PHC=∠ACD=60°, ∠CHN=∠CBE=60°
∴MG= HP,NH= GP,∠MGP=∠PHN=120°
在△MGP和△PHN中
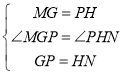
∴△MGP≌△PHN
∴∠MPG=∠PNH
∴∠PNH+∠NPH=180°-∠PHN=60°
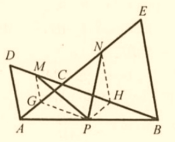
(2)![]() 的度数不变,仍是60°,
的度数不变,仍是60°,
证明:如图所示,取![]() 、
、![]() 的中点分别为
的中点分别为![]() ,
,![]() ,
,
连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
∵![]() 是等边
是等边![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
同理![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
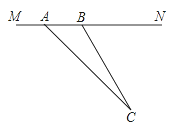
【题目】目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把平面内一条数轴x绕点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在平面斜坐标系中,若θ=45°,点P的斜坐标为(1,2![]() ),点G的斜坐标为(7,﹣2
),点G的斜坐标为(7,﹣2![]() ),连接PG,则线段PG的长度是_____.
),连接PG,则线段PG的长度是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com