
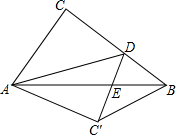
 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$. 分析 点E与点C′重合时.在Rt△ABC中,由勾股定理可求得BC=4,由翻折的性质可知:AE=AC=3、DC=DE.则EB=2.设DC=ED=x,则BD=4-x.在Rt△DBE中,依据勾股定理列方程求解即可;当∠EDB=90时.由翻折的性质可知:AC=AC′,∠C=∠C′=90°,然后证明四边形ACDC′为正方形,从而求得DB=1,然后证明DE∥AC,△BDE∽△BCA,依据相似三角形的性质可求得DE=$\frac{3}{4}$.
解答 解:如图1所示;点E与点C′重合时.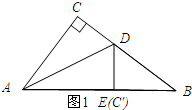
在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4.
由翻折的性质可知;AE=AC=3、DC=DE.则EB=2.
设DC=ED=x,则BD=4-x.
在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2.
解得:x=$\frac{3}{2}$.
∴DE=$\frac{3}{2}$.
如图2所示:∠EDB=90时.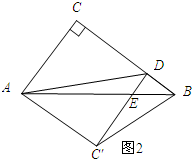
由翻折的性质可知:AC=AC′,∠C=∠C′=90°.
∵∠C=∠C′=∠CDC′=90°,
∴四边形ACDC′为矩形.
又∵AC=AC′,
∴四边形ACDC′为正方形.
∴CD=AC=3.
∴DB=BC-DC=4-3=1.
∵DE∥AC,
∴△BDE∽△BCA.
∴$\frac{DE}{AC}=\frac{DB}{CB}=\frac{1}{4}$,即$\frac{ED}{3}=\frac{1}{4}$.
解得:DE=$\frac{3}{4}$.
点D在CB上运动,∠DBC′<90°,故∠DBC′不可能为直角.
故答案为:$\frac{3}{2}$或$\frac{3}{4}$.
点评 本题主要考查的是翻折的性质、勾股定理、正方形的判定、相似三角形的性质和判定,根据题意画出符合题意的图形是解题的关键.


科目:初中数学 来源: 题型:解答题
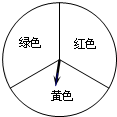 甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色查看答案和解析>>
科目:初中数学 来源: 题型:填空题
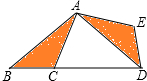 如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.
如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则旋转角∠BAD=100度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
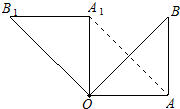 如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1
如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
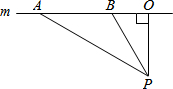 随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-b<b<-a | B. | a<b<-b<-a | C. | -a<-b<b<a | D. | -b<-a<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com