
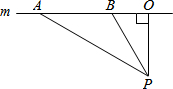
 随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.分析 (1)Rt△OPC与Rt△BOP中,先根据锐角三角函数的定义求出AO及BO的长,再根据AB=AO-BO即可得出结果;
(2)先根据汽车从A到B用时2秒求出其速度,再与已知相比较即可.
解答 解:(1)在Rt△AOP中,∵PO=21米,∠PAO=30°,
∴AO=$\frac{PO}{tan30°}$=$\frac{21}{\frac{\sqrt{3}}{3}}$=21$\sqrt{3}$(米);
在Rt△BOP中,∵PO=21米,∠PBO=60°,
∴BO=$\frac{PO}{tan60°}$=$\frac{21}{\sqrt{3}}$=7$\sqrt{3}$(米),
∴AB=AO-BO=14$\sqrt{3}$米;
(2)这辆校车超速;理由如下:
∵校车从A到B用时2秒,
∴速度为14$\sqrt{3}$÷2=7$\sqrt{3}$(米/秒)>12米/秒,
∴这辆校车在AB路段超速.
点评 此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,注意数形结合思想的应用.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:填空题
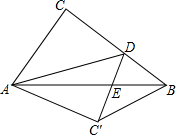 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
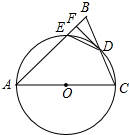 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)2=0 | B. | (x-1)2=1 | C. | (x-1)2=2 | D. | (x+1)2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com