练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
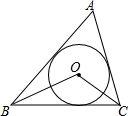
    1．如图，已知⊙O是△ABC的内切圆，且∠ABC=50°，∠ACB=80°，则∠BOC=（　　）
    A．100°B．75°C．115°D．105°

    分析 三角形的内切圆的圆心是三角形三条内角平分线的交点，故此∠OBC=$\frac{1}{2}$∠ABC=25°，∠OCB=$\frac{1}{2}$∠ACB=40°，最后依据三角形的内角和定理求解即可．

    解答 解：∵⊙O是△ABC的内切圆，
    ∴∠OBC=$\frac{1}{2}$∠ABC=25°，∠OCB=$\frac{1}{2}$∠ACB=40°．
    ∴∠BOC=180°-25°-40°=115°．
    故选：C．

    点评 本题主要考查的是三角形的内切圆与内心，明确三角形的内心是三角形三条内角平分线的交点是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．下列各式从左到右的变形，正确的是（　　）
    A．$\frac{y}{x}$=$\frac{{y}^{2}}{{x}^{2}}$B．$\frac{y}{x}$=$\frac{yz}{xz}$（z≠0）C．$\frac{y}{x}$=$\frac{y-m}{x-m}$D．$\frac{y}{x}$=$\frac{y+n}{x+n}$（n≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

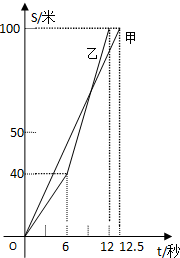    12．甲、乙两同学在一次百米赛跑中，路程S（米）与时间t（秒）之间的关系如图所示．根据图象回答下列问题：
    （1）3-8秒时，哪位同学处于领先位置？
    （2）求甲同学所走的路程S（米）与时间t（秒）之间的函数关系式．
    （3）这次赛跑中，哪位同学先到达终点？比另一个同学早多少时间到达？约几秒后哪位同学被哪位同学追上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．若x2+8x+m是完全平方式，则m的值等于（　　）
    A．16B．8C．4D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图1，已知在Rt△ABC中，AB=BC，∠ABC=90°，O为AC中点．
    （1）如图1，若把三角板的直角顶点放置于点O，两直角边分别与AB、BC交于点M，N，求证：BM=CN；
    （2）若点P是线段AC上一动点，在射线BC上找一点D，使PD=PB，再过点D作BO的平行线，交直线AC于一点E，试在备用图上探索线段ED和OP的关系，并说明理由．试在备用图上探索线段ED和OP的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

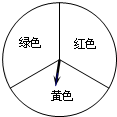    6．甲、乙两位同学玩转盘游戏，游戏规则：将圆盘平均分成三份，分别涂上红，黄，绿三种颜色，两位同学分别转动转盘两次（若压线，重新转）．若两次指针指到的颜色
    相同，则甲获胜；若两次指针指到的颜色是黄绿组合则乙获胜；其余情况则视为平局．
    请用画树状图或列表的方法，用概率说明游戏是否公平．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

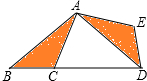    13．如图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至△ADE处，使点B落在BC延长线上的D点处，则旋转角∠BAD=100度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

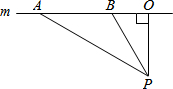    10．随着近几年我市私家车日越增多，超速行驶成为引发交通事故的主要原因之一．某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动，设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点P，在笔直的车道m上确定点O，使PO和m垂直，测得PO的长等于21米，在m上的同侧取点A、B，使∠PAO=30°，∠PBO=60°．
    （1）求A、B之间的路程（保留根号）；
    （2）已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒，这辆校车是否超速？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）-1+（-2）3÷4×（-3）2；
    （2）3（2a+3b）-2（4a-6b）．

    查看答案和解析>>

    同步练习册答案