
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中: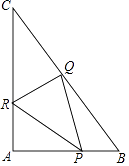
(1)求证:△APR,△BPQ,△CQR的面积相等;
(2)求△PQR面积的最小值;
(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.
【答案】
(1)解:如图,在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,tan∠B= ![]() =
= ![]() =
= ![]()
![]() ,
,
过点Q作QE⊥AB于E,
在Rt△BQE中,BQ=5t,
∴sin∠B= ![]() =
= ![]() ,
,
∴QE=4t,
过点Q作QD⊥AC于D,
在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,
∴QD=CQsin∠C= ![]() (10﹣5t)=3(2﹣t),
(10﹣5t)=3(2﹣t),
由运动知,AP=3t,CR=4t,
∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),
∴S△APR= ![]() APAR=
APAR= ![]() ×3t×4(2﹣t)=6t(2﹣t),
×3t×4(2﹣t)=6t(2﹣t),
S△BPQ= ![]() BPQE=
BPQE= ![]() ×3(2﹣t)×4t=6t(2﹣t),
×3(2﹣t)×4t=6t(2﹣t),
S△CQR= ![]() CRQD=
CRQD= ![]() ×4t×3(2﹣t)=6t(2﹣t),
×4t×3(2﹣t)=6t(2﹣t),
∴S△APR=S△BPQ=S△CQR,
∴△APR,△BPQ,△CQR的面积相等;
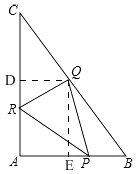
(2)解:由(1)知,S△APR=S△BPQ=S△CQR=6t(2﹣t),
∵AB=6,AC=8,
∴S△PQR=S△ABC﹣(S△APR+S△BPQ+S△CQR)
= ![]() ×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,
×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,
∵0≤t≤2,
∴当t=1时,S△PQR最小=6;
(3)解:存在,由点P,Q,R的运动速度知,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,此时,四边形APQR是矩形,即:t=1秒时,∠PQR=90°,
由(1)知,QE=4t,QD=3(2﹣t),AP=3t,CR=4t,AR=4(2﹣t),
∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),
过点Q作QD⊥AC于D,作QE⊥AB于E,∵∠A=90°,
∴四边形APQD是矩形,
∴AE=DQ=3(2﹣t),AD=QE=4t,
∴DR=|AD﹣AR|=|4t﹣4(2﹣t)|=4|2t﹣2|,PE=|AP﹣AE|=|3t﹣3(2﹣t)|=3|2t﹣2|
∵∠DQE=90°,∠PQR=90°,
∴∠DQR=∠EQP,
∴tan∠DQR=tan∠EQP,
在Rt△DQR中,tan∠DQR= ![]() =
= ![]() ,
,
在Rt△EQP中,tan∠EQP= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴16t=9(2﹣t),
∴t= ![]() .
.
即:t=1或 ![]() 秒时,∠PQR=90°.
秒时,∠PQR=90°.
【解析】(1)由面积公式可知求三角形的面积,缺高时,须作垂线补出高,用t的代数式表示△APR,△BPQ,△CQR的面积,在由斜边表示直角边时选用正弦;(2)用△ABC面积减去第(1)问中表示的△APR的面积的3倍,构建二次函数,在0≤t≤2范围内由二次函数的性质可求最值;(3)由点P,Q,R的运动速度知,3![]() 6=
6=![]() ,5
,5![]() 10=
10=![]() ,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,可证得四边形APQD是矩形,∠PQR=90°;若∠PQR=90
,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,可证得四边形APQD是矩形,∠PQR=90°;若∠PQR=90![]() ,则∠DQR=∠EQP,用t的代数式表示两个角的正切,建立方程,求出t.
,则∠DQR=∠EQP,用t的代数式表示两个角的正切,建立方程,求出t.
【考点精析】通过灵活运用二次函数的最值和锐角三角函数的定义,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、c满足|a+2|+(c-7)2=0.
![]()
(1)a=______,b=______,c=______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB=______,AC=______,BC=______.(用含t的代数式表示).
(4)直接写出点B为AC中点时的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1)(3,5,7)、(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A89=( )
A.(6,7)
B.(7,8)
C.(7,9)
D.(6,9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)解不等式﹣x+1<7x﹣3;
(2)解不等式![]() ;
;
(3)解不等式![]() ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.
(4)已知关于x的不等式组 ,恰好有两个整数解,试确定实数a的取值范围.
,恰好有两个整数解,试确定实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是

A. 50° B. 80° C. 100° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,共顶点的两个三角形△ABC,△AB′C′,若 AB=AB′,AC=AC′,且∠BAC+∠B′AC′=180°,我们称△ABC 与△AB′C′互为“顶补三角形”.
(1)已知△ABC 与△ADE 互为“顶补三角形”,AF 是△ABC 的中线.
①如图 2,若△ADE 为等边三角形时,求证:DE=2AF;
②如图 3,若△ADE 为任意三角形时,上述结论是否仍然成立?请说明理由.

(2)如图4,四边形 ABCD 中,∠B+∠C=90°.在平面内是否存在点 P,使△PAD 与△PBC 互为“顶补三角形”, 若存在,请画出图形,并证明;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com