
【题目】解答下列各题:
(1)解不等式﹣x+1<7x﹣3;
(2)解不等式![]() ;
;
(3)解不等式![]() ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.
(4)已知关于x的不等式组 ,恰好有两个整数解,试确定实数a的取值范围.
,恰好有两个整数解,试确定实数a的取值范围.
【答案】(1)![]() ; (2)x≤﹣2;(3)x≤﹣1;(4)﹣
; (2)x≤﹣2;(3)x≤﹣1;(4)﹣![]() <a≤0.
<a≤0.
【解析】
(1)移项、合并同类项、系数化为1可得;
(2)去分母、去括号、移项、合并同类项、系数化为1可得;
(3)去分母、去括号、移项、合并同类项、系数化为1可得;
(4)首先解不等式组求得解集,然后根据不等式组只有两个整数解,确定整数解,则可以得到一个关于a的不等式组求得a的范围.
解:(1)﹣x﹣7x<﹣3﹣1,
﹣8x<﹣4,
x>![]() ;
;
(2)2(1﹣2x)≥4﹣3x,
2﹣4x≥4﹣3x,
﹣4x+3x≥4﹣2,
﹣x≥2,
x≤﹣2;
(3)3(x+1)﹣2(x﹣2)≤6,
3x+3﹣2x+4≤6,
3x﹣2x≤6﹣3﹣4,
x≤﹣1,
将解集表示在数轴上如下:

(4)解不等式3+4(x+1)>1,得:x>﹣![]() ,
,
解不等式a﹣![]() >﹣1,得:x<2a+1,
>﹣1,得:x<2a+1,
∵不等式组恰有2个整数解,
∴0<2a+1≤1,
解得:﹣![]() <a≤0.
<a≤0.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
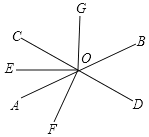
【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=![]()
C. ∠AEC= ![]() ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中: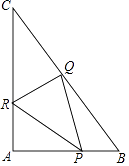
(1)求证:△APR,△BPQ,△CQR的面积相等;
(2)求△PQR面积的最小值;
(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从![]() 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com