
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)解不等式﹣x+1<7x﹣3;
(2)解不等式![]() ;
;
(3)解不等式![]() ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.
(4)已知关于x的不等式组 ,恰好有两个整数解,试确定实数a的取值范围.
,恰好有两个整数解,试确定实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径AE平分弦CD,交CD于点G,EF∥CD,交AD的延长线于F,AP⊥AC交CD的延长线于点P.
(1)求证:EF是⊙O的切线;
(2)若AC=2,PD= ![]() CD,求tan∠P的值.
CD,求tan∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,共顶点的两个三角形△ABC,△AB′C′,若 AB=AB′,AC=AC′,且∠BAC+∠B′AC′=180°,我们称△ABC 与△AB′C′互为“顶补三角形”.
(1)已知△ABC 与△ADE 互为“顶补三角形”,AF 是△ABC 的中线.
①如图 2,若△ADE 为等边三角形时,求证:DE=2AF;
②如图 3,若△ADE 为任意三角形时,上述结论是否仍然成立?请说明理由.

(2)如图4,四边形 ABCD 中,∠B+∠C=90°.在平面内是否存在点 P,使△PAD 与△PBC 互为“顶补三角形”, 若存在,请画出图形,并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,其运用到的数学原理是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点有且只有一条直线和已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
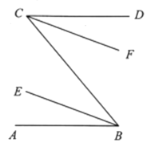
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,已知![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,求证:
,求证:![]() .
.
证明:∵AB//CD,(已知)
∴∠ABC=∠______.(两直线平行,内错角相等)
∵__________.(已知)
∴∠EBC=![]() ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)
同理,∠FCB=______.
∵∠EBC=∠FCB.(等量代换)
∴BE//CF.(____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90。 , AB=6,sinC= ![]() ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于![]() BM长为半径作弧,两弧相交于N,射线AN与BC相交于D,则AD的长为 .
BM长为半径作弧,两弧相交于N,射线AN与BC相交于D,则AD的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com