
【题目】如图,直径AE平分弦CD,交CD于点G,EF∥CD,交AD的延长线于F,AP⊥AC交CD的延长线于点P.
(1)求证:EF是⊙O的切线;
(2)若AC=2,PD= ![]() CD,求tan∠P的值.
CD,求tan∠P的值.
【答案】
(1)证明:∵直径AE平分弦CD,
∴AG⊥CD(垂径定理).
∵EF∥CD(已知),
∴∠AEF=∠AGD=90°.
∴EF是⊙O的切线.
(2)∵∠CAP=∠AGC=90°,∠ACG=∠PCA.
∴△CAG∽△CPA(AA).
∴AC2=CGCP(相似三角形的对应边成比例).
又∵PD= ![]() CD(已知),
CD(已知),
CG=GD,
∴CG= ![]() PC.而AC=2,
PC.而AC=2,
∴22= ![]() PCPC,∴PC2=12.
PCPC,∴PC2=12.
又∵AC⊥AP,∴AP2=PC2﹣AC2(勾股定理),
∴AP= ![]() .(13分)
.(13分)
∴tan∠P= ![]() .
.
【解析】(1)要证EF是⊙O的切线,只需证明∠AEF=90°即可.(2)首先利用相似三角形判定定理证明△CAG∽△CPA,利用性质:对应边成比例,得到AC2=CGCP,求得PC2=12,在直角三角形APC中利用勾股定理求得AP的长度,进而利用三角函数的定义求tan∠P的值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=![]()
C. ∠AEC= ![]() ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,现有一个长方体水槽放在桌面上,从水槽内量得它的侧面高20cm,底面的长25cm,宽20cm,水槽内水的高度为acm,往水槽里放入棱长为10cm的立方体铁块.
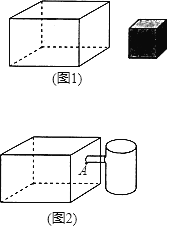
(1)求下列两种情况下a的值.
①若放入铁块后水面恰好在铁块的上表面;
②若放入铁块后水槽恰好盛满(无溢出).
(2)若0<a≤18,求放入铁块后水槽内水面的高度(用含a的代数式表示).
(3)如图2,在水槽旁用管子连通一个底面在桌面上的圆柱形容器,内部底面积为50cm2,管口底部A离水槽内底面的高度为hcm(h>a),水槽内放入铁块,水溢入圆柱形容器后,容器内水面与水槽内水面的高度差为8.2cm,若a=15,求h的值.(水槽和容器的壁及底面厚度相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.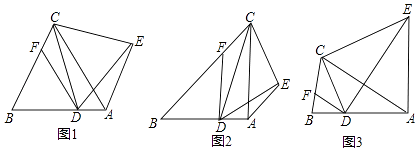
(1)如图1,当α=60°时,求证:△DCE是等边三角形.
(2)如图2.当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系(用α表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:

(1)用一种正多边形镶嵌平面
例如,用 6 个全等的正三角形镶嵌平面,摆放方案如图所示:
若用 m 个全等的正 n 边形镶嵌平面,求出 m,n 应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个,设这 n 个正多边形的边数分别为 x1,x2,…,xn,求出 x1,x2,…,xn 应满足的关系式.(用含 n 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.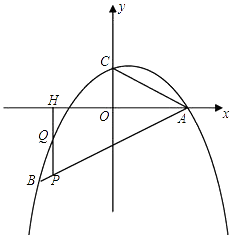
(1)试求此二次函数的解析式;
(2)试证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com