
【题目】如图1,共顶点的两个三角形△ABC,△AB′C′,若 AB=AB′,AC=AC′,且∠BAC+∠B′AC′=180°,我们称△ABC 与△AB′C′互为“顶补三角形”.
(1)已知△ABC 与△ADE 互为“顶补三角形”,AF 是△ABC 的中线.
①如图 2,若△ADE 为等边三角形时,求证:DE=2AF;
②如图 3,若△ADE 为任意三角形时,上述结论是否仍然成立?请说明理由.

(2)如图4,四边形 ABCD 中,∠B+∠C=90°.在平面内是否存在点 P,使△PAD 与△PBC 互为“顶补三角形”, 若存在,请画出图形,并证明;若不存在,请说明理由.

【答案】(1) ①见解析 ②成立,理由见解析(2)存在点P,证明见解析.
【解析】
(1)①首先证明![]() ,再利用
,再利用![]() 与
与![]() 互为“顶补三角形”,求得
互为“顶补三角形”,求得![]() ,
,![]() ,再利用
,再利用![]() 是
是![]() 的中线和
的中线和![]() ,即可证得;
,即可证得;
②首先证明![]() ,然后根据
,然后根据![]() ,证得
,证得![]() ,再根据全等三角形对应边相等即可解决问题;
,再根据全等三角形对应边相等即可解决问题;
(2)先做辅助线![]() ,
,![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 则的交点
则的交点![]() ,然后利用垂直平分线定理,即可解决问题.
,然后利用垂直平分线定理,即可解决问题.
证明:(1)①如图25-1,
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]()
![]() 与
与![]() 互为“顶补三角形”,
互为“顶补三角形”,
![]() ,
,![]()
![]() 是
是![]() 的中线,
的中线,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
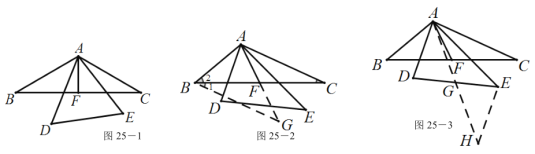
②方法一:如图25-2,
延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,
![]() 是
是![]() 的中线,
的中线,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
, ![]()
即![]() ;方法二:如图25-3,
;方法二:如图25-3,
取![]() 中点
中点![]() ,连接
,连接![]() ,并延长到
,并延长到![]() ,使
,使![]() ,连接
,连接![]() 可证得
可证得![]() ,
, ![]() ,(方法同上)
,(方法同上)
又由![]() 是
是![]() 的中线,
的中线,![]() 是
是![]() 的中线,
的中线,
![]() ;
;
(2)存在点![]() .如图25-4,分别作线段
.如图25-4,分别作线段![]() ,
,![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 则的交点
则的交点![]() ,使得
,使得![]() 与
与![]() 互为“顶补三角形”.
互为“顶补三角形”.
证明:延长![]() ,
,![]() 交于点
交于点![]() .
.
![]() ,
,
![]() ,
,
![]() 垂直平分
垂直平分![]() 于点
于点![]() ,
,![]() 垂直平分
垂直平分![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,
![]() ,
,
综上所述,![]() 与
与![]() 互为“顶补三角形”.
互为“顶补三角形”.


科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中: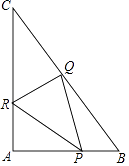
(1)求证:△APR,△BPQ,△CQR的面积相等;
(2)求△PQR面积的最小值;
(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.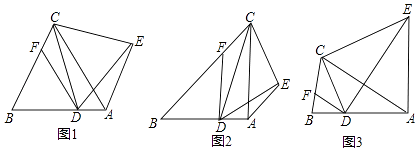
(1)如图1,当α=60°时,求证:△DCE是等边三角形.
(2)如图2.当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系(用α表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:

(1)用一种正多边形镶嵌平面
例如,用 6 个全等的正三角形镶嵌平面,摆放方案如图所示:
若用 m 个全等的正 n 边形镶嵌平面,求出 m,n 应满足的关系式;
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案;
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个,设这 n 个正多边形的边数分别为 x1,x2,…,xn,求出 x1,x2,…,xn 应满足的关系式.(用含 n 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com