
���� ��1�����ȸ������⻭����״ͼ��Ȼ������״ͼ�ó����п��ܵĽ����ע���ǷŻ�ʵ�黹�Dz��Ż�ʵ�飻
��2���ɱ���������еȿ��ܵĽ��������x��y����y=x������������ø��ʹ�ʽ��⼴����ô𰸣�
��� �⣺��1��
�б��ã�
| 1 | 2 | 3 | 4 | |
| 1 | ��1��1�� | ��2��1�� | ��3��1�� | ��4��1�� |
| 2 | ��1��2�� | ��2��2�� | ��3��2�� | ��4��2�� |
| 3 | ��1��3�� | ��2��3�� | ��3��3�� | ��4��3�� |
| 4 | ��1��4�� | ��2��4�� | ��3��4�� | ��4��4�� |
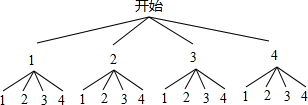
���� ���⿼��������б�������״ͼ������ʣ�ע�����ַŻ��벻�Ż�ʵ�飬�б�������״ͼ�����Բ��ظ�����©���г����п��ܵĽ�����õ���֪ʶ��Ϊ������=������������������֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x2-2x-4=0 | B�� | x2-x+1=0 | C�� | x2-3x=0 | D�� | x2+2x+1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F��BD��AE��AF����G��H��
��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F��BD��AE��AF����G��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ��ת�̣�ת�̱�ƽ���ֳ�4�ȷݣ������ֳ�4����С��ȵ����Σ�4�����ηֱ��������1��2��3��4��ָ���λ�ù̶���ת��ת�̺���������ֹͣ��ÿ��ָ������ÿһ���εĻ�����ȣ���ָ��ǡ�����ڷֽ���������ת����
��ͼ��һ��ת�̣�ת�̱�ƽ���ֳ�4�ȷݣ������ֳ�4����С��ȵ����Σ�4�����ηֱ��������1��2��3��4��ָ���λ�ù̶���ת��ת�̺���������ֹͣ��ÿ��ָ������ÿһ���εĻ�����ȣ���ָ��ǡ�����ڷֽ���������ת�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com