
【题目】将下列各式因式分解:
(1)![]() .
.
(2)![]() .
.
(3)3x(x-y)3-6y(y-x)2.
(4)![]() .
.
(5)![]() .
.
(6)(a+4)(a﹣4)+3(a+2).
【答案】(1)3x(x+3)(x-3);(2)(a-2+c)(a-2-c);(3)3(x-y)![]() (x
(x![]() -xy-2y);(4)4(3a+b)(-a-3b);(5)(2﹣3x+3y)
-xy-2y);(4)4(3a+b)(-a-3b);(5)(2﹣3x+3y)![]() ;(6)(a+5)(a﹣2).
;(6)(a+5)(a﹣2).
【解析】
(1)先提取公因式3x,再利用平方差公式分解因式即可;(2)先利用完全平方公式把前3项分解因式,再利用平方差公式分解因式即可;(3)直接提取公因式3(x-y)2分解因式即可;(4)先提取公因式4,再利用平方差公式分解因式即可;(5)直接利用完全平方公式分解因式即可;(6)先利用平方差公式展开,合并,再利用十字相乘法分解因式即可.
(1)![]() =3x(x2-9)=3x(x+3)(x-3)
=3x(x2-9)=3x(x+3)(x-3)
(2)![]() =(a-2)2-c2=(a-2+c)(a-2-c)
=(a-2)2-c2=(a-2+c)(a-2-c)
(3)3x(x-y)3-6y(y-x)2=3(x-y)2[x(x-y)-2y]=3(x-y)2(x2-xy-2y).
(4)![]() =4[(a-b)2-4(a+b)2]=4(a-b+2a+2b)(a-b-2a-2b)=4(3a+b)(-a-3b).
=4[(a-b)2-4(a+b)2]=4(a-b+2a+2b)(a-b-2a-2b)=4(3a+b)(-a-3b).
(5)![]() =[2-3(x-y)]2=(2-3x+3y)2.
=[2-3(x-y)]2=(2-3x+3y)2.
(6)(a+4)(a﹣4)+3(a+2)=a2-16+3a+6=a2+3a-10=(a+5)(a-2).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】问题探究
(1)在 6 月份的日历中(如图 1),任意圈出一列上相邻的三个数,设中间的一个数为 a,则用含 a 的代数式表示这三个数(从小到大)分别是________________________________ .
(2)连续的自然数 1 至 2004 按图中的方式派成一个长方形阵列,用一个正方形框出 16 个数(如图2)
①图2中框出的这 16 个数之和是____________;
②在图2中,要使一个正方形框出的 16 个数之和分别等于 839、2000,是否可能?若不可能,试说明理由.若有可能,请求出该正方形框出的 16 个数中的最小数与最大数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
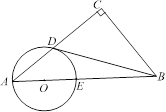
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).
(1)在所给的平面直角坐标系中画出它的图象并求一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB=![]() S△AOB,求P点的坐标.
S△AOB,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(9x3y-12xy3+3xy2)÷(-3xy)-(2y+x)(2y-x),其中x=1,y=-2;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m、n满足方程组![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴上,边
轴正半轴上,边![]() ,
,![]() (
(![]() )的长分别是方程
)的长分别是方程![]() 的两个根,
的两个根,![]() 是边
是边![]() 上的一动点(不与A、B重合).
上的一动点(不与A、B重合).
(1)填空:AB= ,OA= .
(2)若动点D满足△BOC与△AOD相似,求直线![]() 的解析式.
的解析式.
(3)若动点D满足![]() ,且点
,且点![]() 为射线
为射线![]() 上的一个动点,当△PAD是等腰三角形时,直接写出点
上的一个动点,当△PAD是等腰三角形时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com